A general overview of secret sharing and Shamir’s secret sharing algorithm

In this writeup, I’m going to talk about what secret sharing is and dive into the details of a popular secret sharing algorithm, Shamir’s secret sharing. Essentially, secret sharing examines how to distribute some secret information among a group of parties in a secure manner, without compromising the ability for authorized groups to recover the secret.

Secret sharing plays a critical role in privacy-preserving data science, where multiple parties may want to pool their data for aggregate analysis without revealing their individual data values.

Some example use cases include:

• Medical research: multiple hospitals may wish to pool patient data to train models for disease forecasting, without revealing sensitive patient information to satisfy regulatory requirements.
• Financial analysis: multiple financial institutions may be willing to pool data to perform some market analysis, while keeping their individual positions private.

By splitting the sensitive data into secret shares, parties may pool their data for aggregate analysis without revealing the original values of the sensitive data in the process.

Contents

• What is secret sharing?
• Introduction: Shamir’s Secret Sharing
• Example: Shamir’s (2, n) Secret Sharing
• Extending to (t, n)
• Properties of Shamir’s Secret Sharing
• Implementation in Code
• Wrap-up
• Sources

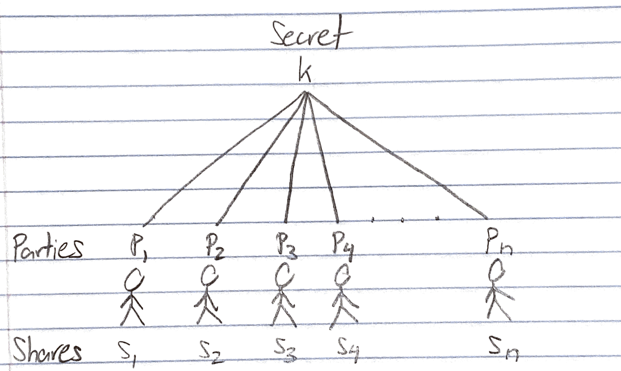
What is secret sharing?

Suppose we have some secret information, k, that we wish to split into shares, s_1,…, s_n, to distribute among n parties, P_1,…, P_n. We want the shares to satisfy the following properties:

• Any subset of t ≤ n parties, where t is some threshold we specify beforehand, may aggregate their shares in some manner to reconstruct k.
• No subset of less than t parties may pool their shares to derive any intelligible information about k.

Let’s look at a simple example of additive secret sharing.

• Suppose we have some secret number, z, we want to split into shares among 3 parties.
• Specifically, let’s define z = w + x + y, where w, x, y are the shares of parties P_1, P_2, and P_3, as depicted below. The participant shares may be any real number.

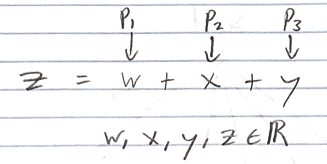
Clearly, no single share or pair of shares reveals any intelligible information about the value of z.

• Let’s say we know the shares for P_1 and P_2.
• For all we know, P_3’s share may be any real number. So, any real number is still equally likely to be the value of the original secret. Thus, the shares for all 3 participants are required to determine the original secret.
• This is an example of an (n, n), specifically (3, 3), secret sharing scheme.

Introduction: Shamir’s Secret Sharing

Let’s consider how to build a general (t, n) secret sharing scheme.

• We want to split some secret k among n parties.
• Establish some threshold t ≤ n such that any subset of t shares may be aggregated in some manner to reconstruct k.
• No subset of t-1 shares provides sufficient information for reconstructing k.

How can we construct such a scheme? Enter Shamir’s secret sharing!

Shamir’s secret sharing scheme uses polynomials to construct a (t, n) scheme efficiently.

• Recall that any t-1 degree polynomial may be uniquely identified by t distinct points. For example, 2 points define a straight line, 3 points define a quadratic, etc.
• A (t, n) scheme requires the secret to be reconstructed by t points. So, we’ll generate a random polynomial p of degree t-1 for the (t, n) scheme, and place the secret value k at the y-intercept i.e. p(0) = k.
• Define the shares for the n parties to be n distinct points evaluated on that polynomial p. For example, the shares may be p(1), p(2),…, p(n).
• Distribute these shares to the corresponding parties. Notice that any subset of t parties may pool their share values to derive the coefficients of p, since p is a t-1 degree polynomial.
• Once the coefficients of p are known, the parties may derive the secret by evaluating p(0) = k.

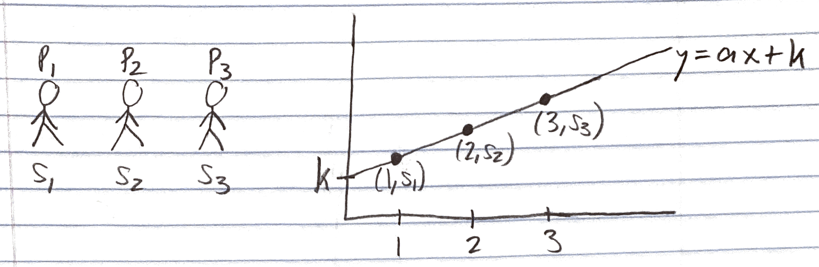
Example: Shamir’s (2, n) Secret Sharing

Let’s walk through how we would use Shamir’s secret sharing to construct a (2, n) secret sharing scheme.

Suppose we have secret k to distribute into n shares, s_1,…, s_n, among n parties, P_1,…, P_n.

• In a (2, n) scheme, any 2 points should uniquely define the polynomial p used for computing the shares.
• So, we’ll generate a random degree 1 polynomial (i.e. a straight line), such that p(0) = k. Specifically, let’s define p(x) = a*x + k, where a ∈ ℕ.
• Compute n shares s_1,…, s_n, such that s_i = p(i) = a*i + k, ∀i={1,…, n}.
• Distribute share s_i to party P_i, ∀i={1,…, n}.

Note: in practice, the protocol requires establishing some large prime number g, over which all coefficients and computations are to be completed within the finite field defined by g. However, omitting that detail doesn’t change the intuition/major steps of the protocol.

Is this (2, n) secret sharing scheme correct? Can we pick any pair of shares to derive k?

• Consider parties P_i, P_j, with shares s_i = a*i + k, s_j = a*j + k, respectively.
• We can represent this pooled information as a system of equations with 2 equations, 2 unknowns.

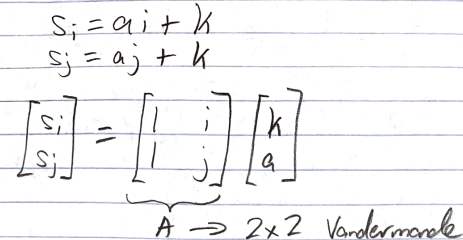
• Notice that A (defined above) is a 2 x 2 Vandermonde matrix such that det(A) = j — i ≠ 0, i.e. A is invertible.
• Thus, we may derive the polynomial by multiplying the inverse of A to both sides, recovering secret k in the process.

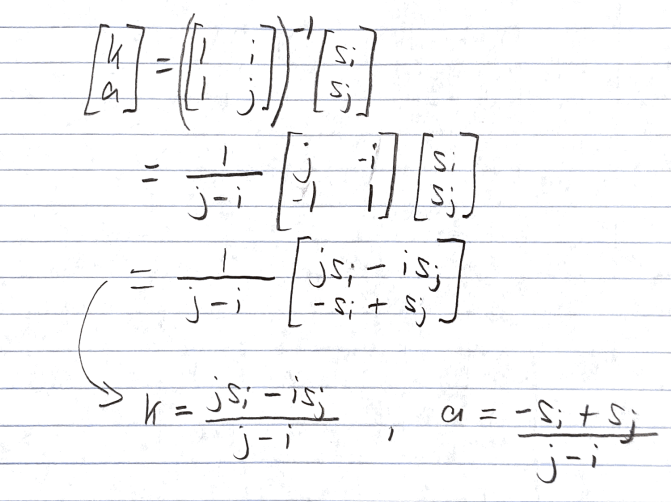
Is this (2, n) secret sharing scheme secure? That is, no single share provides sufficient information to derive k?

Let’s consider the viewpoint of a single party P_i in this protocol.

• P_i knows their own share s_i = a*i + k. Since no other parties are pooling shares, P_i has no knowledge about the other shares s_j, ∀j ≠ i.
• Recall: a is some random non-zero integer. Therefore, a*i is also indistinguishable from some random non-zero integer.
• Thus, s_i = a*i + k is the sum of some number k with some number, a*i, which is indistinguishable from random. So, it follows that s_i is also indistinguishable from random, thus revealing no intelligible information about k.

Extending to (t, n)

Let’s extend the example above to construct a (t, n) secret sharing scheme.

The steps are the same as the (2, n) example above, the only difference being that the polynomial we use to define the shares must be uniquely defined by any t points.

• Thus, let’s generate a random degree t-1 polynomial, p, such that p(0) = k. Specifically, define p(x) = a_{t-1}*x^{t-1} +…+ a_1*x + k, where a_i ∈ ℤ, and a_{t-1} ≠ 0.
• Define P_i’s share, s_i, such that s_i = p(i) = a_{t-1}*i^{t-1} +…+ a_1*i + k, ∀ i={1,…, n}.

Let’s examine the correctness of this (t, n) scheme. Does any subset of t shares provide sufficient information to derive secret k?

• Consider parties P_1,…,P_t who wish to pool their shares s_1,…, s_t to derive k.
• We can represent this information with the following system of t equations, t unknowns.

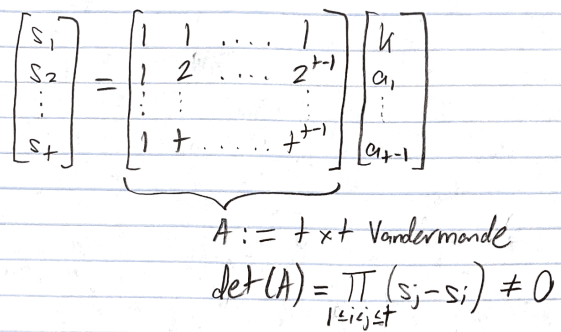
• A is a t x t Vandermonde matrix such that det(A) = Π(s_j — s_i), ∀i ≠ j. It turns out that this sequential product is non-zero, i.e. A is invertible. Check this out if you’re interested in the proof behind the non-zero determinant of any square Vandermonde matrix.
• Thus, we can multiply both sides by the inverse of A and solve the system below to derive polynomial p and secret k.

Let’s examine the security of this (t, n) scheme. Does it hold that no subset of t-1 shares provides sufficient information to derive secret k?

• Consider t-1 parties P_1,…,P_{t-1} who wish to pool their shares s_1,…, s_{t-1}.
• We can represent this information with the following system of equations:

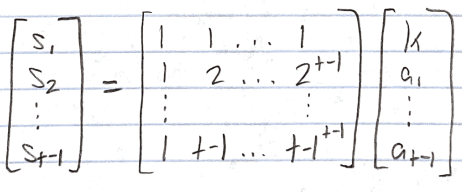
• Notice the system above contains t-1 equations and t unknown parameters.
• Therefore, we can vary one of these parameters (secret k) freely while still satisfying the point constraints s_1,…, s_{t-1}. In other words, any value of k ∈ ℝ is equally likely to be the intercept of a polynomial that contains those shares s_1,…, s_{t-1}.

Properties of Shamir’s Secret Sharing

The examples above illustrated how Shamir’s secret sharing is information-theoretically secure i.e. no subset of parties smaller than the established threshold, t, may derive any intelligible information about k. Let’s look at some additional properties of Shamir’s secret sharing.

Once a (t, n) secret sharing scheme is established, it may be easily extended to additional parties.

• If new parties want to participate in the secret sharing scheme, we can simply generate new shares by evaluating more points on the defining polynomial ex: s_{i+1} = p(i+1), s_{i+2} = p(i+2), etc.
• This changes nothing about the security guarantees of the secret sharing scheme, as the degree of the defining polynomial remains the same.

However, once a share is established for a participating party, there is no way to “invalidate” their share from the pool of other shares.

• Consider some organization A, who has some secret information, k, split among members internal to the organization via Shamir’s (t, n) secret sharing.
• If any subset of these t members leaves the organization, they may pool their shares to derive k, leaking k external to the organization.
• Preventing this would require re-executing the Shamir protocol periodically to define a new random polynomial for recomputing shares and redistributing them to the relevant parties.

For more information about properties/consequences of Shamir’s secret sharing, I highly recommend this read.

Implementation in Code

Below is a basic python implementation of Shamir’s (t, n) secret sharing as we discussed here. All the relevant methods implementing the algorithmic logic behind Shamir’s secret sharing are included below. Some unrelated utility functions are omitted to keep it concise.

Feel free to check out the Github below.

GitHub – jimin-kang/Shamir-Secret-Sharing

import random # in practice, this should be cryptographically secure
import numpy as np
from numpy.polynomial import polynomial as P
from prompt_inputs import accept_scheme_parameters, prompt_pooled_parties

# prime number to define the finite field where coefficients will be sampled from
# in practice, FIELD_SIZE > max(n, k)  
FIELD_SIZE = 65521

def generate_polynomial(d, k):
    """
    Parameters:
        d: degree of polynomial to be generated
        k: secret to define polynomial y-intercept
    Returns:
        poly: vector of polynomial coefficients & intercept
               ordered from intercept term to largest degree term i.e. [k, a_{1}, a_{2},..., a_{t-1}]
    """
    # generate random coeffcients from {0,...,p-1}
    poly = [random.randint(0, FIELD_SIZE-1) for _ in range(d)]

    # coefficient of largest degree term must be non-zero
    poly[-1] = random.randint(1, FIELD_SIZE-1)

    # place secret at y-intercept i.e. p(0) = k
    poly.insert(0, k)

    return poly

def compute_shares(poly, n):
    """
    Parameters:
        coeff: polynomial coefficients ordered from intercept term to largest degree term i.e. [k, a_{1}, a_{2},..., a_{t-1}]
        n: number of parties to distribute secret shares to
    Returns:
        shares: vector of computed shares
                ordered by ascending order of party index i.e. [s_{1}, s_{2},..., s_{n}]
    """
    # evaluate polynomial at x in {1, 2,..., n}
    x = np.arange(1, n + 1, 1)

    # Generate the Vandermonde matrix
    vandermonde = P.polyvander(x=x, deg=len(poly)-1)

    # shares = vandermonde * poly
    shares = vandermonde @ poly
    
    return shares

def reconstruct_secret(shares, indices):
    """
    Parameters:
        shares: pooled share values 
        indices: parties corresponding to pooled share values
    Returns:
        secret & vector containing polynomial coefficients and secret
    """
    # Vandermonde matrix for pooled parties
    vandermonde = P.polyvander(x=indices, deg=len(indices)-1)

    # coeff = inv(Vandermonde) * shares
    poly = np.linalg.inv(vandermonde) @ np.array(shares)

    # rounding to deal w/ floating pt. precision errors: wrapping integer lists into numpy arrays may promote integers into floats
    # polynomial coefficients are integers in {0,...,p-1}
    poly = [float(poly[0])] + [round(x) for x in poly[1:]]
    
    print(f"Reconstructed Secret: {poly[0]}")
    print(f"Reconstructed Polynomial: {poly}")

def display_scheme_info(k, poly, shares):
    """
    Display secret (k), polynomial, and shares for the participating parties in the (t, n) secret sharing scheme.
    """
    print(f"Secret: {k}")
    print(f"Polynomial: {poly}")
    print("Shares:")
    for i, share in enumerate(shares):
        print(f"  Party {i+1}: {share}")

def main():
    # define scheme & compute/distribute shares
    t, n, k = accept_scheme_parameters()
    poly = generate_polynomial(t-1, k)
    shares = compute_shares(poly, n)
    
    display_scheme_info(k, poly, shares)

    # prompt for shares to pool
    pooled_parties = prompt_pooled_parties(t, n)
    pooled_shares = [shares[i-1] for i in pooled_parties]
    
    # reconstruct secret from pooled shares
    reconstruct_secret(pooled_shares, pooled_parties)    

Wrap-up

Thanks for reading! A brief recap about what we talked about:

• Secret sharing is a method for parties to distribute some secret information among themselves such that any sufficiently large subset of parties may recover the secret, but no smaller subset may derive any intelligible information about the secret.
• Shamir’s secret sharing scheme is a specific secret sharing algorithm that is information theoretically secure. The scheme uses random polynomials to compute secret shares and invertible matrices to recover the secret.

Shamir’s secret sharing scheme is one that nearly always comes up in any discussion about secret sharing due to its efficiency and unconditional security, but other efficient secret sharing algorithms are used in practice as well. For more information about other secret sharing algorithms, or if you’d like to explore Shamir’s secret sharing at a deeper level, check out the resources below!

Sources

Secret sharing)

• MIT 6.875 (Fall 2023)
• GeeksForGeeks, Additive Secret Sharing
• Farid Hajji, How to Share a Secret
• Adi Shamir, How to Share a Secret
• Wikipedia, Secret Sharing

Vandermonde matrix)

• Wikipedia, Vandermonde Matrix
• Mathematics Stack Exchange, Find N degree polynomial from N+1 points
• Mathematics Stack Exchange, Vandermonde determinant by induction

Applications to privacy-preserving data science)

• Ghavamipour, A.R., Turkmen, F. & Jiang, X. Privacy-preserving logistic regression with secret sharing. BMC Med Inform Decis Mak 22, 89 (2022)
• Jia Duan, Jiantao Zhou, Yuanman Li,
  Privacy-Preserving distributed deep learning based on secret sharing,
  Information Sciences, Volume 527, 2020, Pages 108–127

---

How to Share a Secret: Shamir’s Secret Sharing was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

​A general overview of secret sharing and Shamir’s secret sharing algorithmIn this writeup, I’m going to talk about what secret sharing is and dive into the details of a popular secret sharing algorithm, Shamir’s secret sharing. Essentially, secret sharing examines how to distribute some secret information among a group of parties in a secure manner, without compromising the ability for authorized groups to recover the secret.Secret sharing plays a critical role in privacy-preserving data science, where multiple parties may want to pool their data for aggregate analysis without revealing their individual data values.Some example use cases include:Medical research: multiple hospitals may wish to pool patient data to train models for disease forecasting, without revealing sensitive patient information to satisfy regulatory requirements.Financial analysis: multiple financial institutions may be willing to pool data to perform some market analysis, while keeping their individual positions private.By splitting the sensitive data into secret shares, parties may pool their data for aggregate analysis without revealing the original values of the sensitive data in the process.ContentsWhat is secret sharing?Introduction: Shamir’s Secret SharingExample: Shamir’s (2, n) Secret SharingExtending to (t, n)Properties of Shamir’s Secret SharingImplementation in CodeWrap-upSourcesWhat is secret sharing?Suppose we have some secret information, k, that we wish to split into shares, s_1,…, s_n, to distribute among n parties, P_1,…, P_n. We want the shares to satisfy the following properties:Any subset of t ≤ n parties, where t is some threshold we specify beforehand, may aggregate their shares in some manner to reconstruct k.No subset of less than t parties may pool their shares to derive any intelligible information about k.Image by authorLet’s look at a simple example of additive secret sharing.Suppose we have some secret number, z, we want to split into shares among 3 parties.Specifically, let’s define z = w + x + y, where w, x, y are the shares of parties P_1, P_2, and P_3, as depicted below. The participant shares may be any real number.Additive secret sharing. Image by authorClearly, no single share or pair of shares reveals any intelligible information about the value of z.Let’s say we know the shares for P_1 and P_2.For all we know, P_3’s share may be any real number. So, any real number is still equally likely to be the value of the original secret. Thus, the shares for all 3 participants are required to determine the original secret.This is an example of an (n, n), specifically (3, 3), secret sharing scheme.Introduction: Shamir’s Secret SharingLet’s consider how to build a general (t, n) secret sharing scheme.We want to split some secret k among n parties.Establish some threshold t ≤ n such that any subset of t shares may be aggregated in some manner to reconstruct k.No subset of t-1 shares provides sufficient information for reconstructing k.How can we construct such a scheme? Enter Shamir’s secret sharing!Shamir’s secret sharing scheme uses polynomials to construct a (t, n) scheme efficiently.Recall that any t-1 degree polynomial may be uniquely identified by t distinct points. For example, 2 points define a straight line, 3 points define a quadratic, etc.A (t, n) scheme requires the secret to be reconstructed by t points. So, we’ll generate a random polynomial p of degree t-1 for the (t, n) scheme, and place the secret value k at the y-intercept i.e. p(0) = k.Define the shares for the n parties to be n distinct points evaluated on that polynomial p. For example, the shares may be p(1), p(2),…, p(n).Distribute these shares to the corresponding parties. Notice that any subset of t parties may pool their share values to derive the coefficients of p, since p is a t-1 degree polynomial.Once the coefficients of p are known, the parties may derive the secret by evaluating p(0) = k.Example: Shamir’s (2, n) Secret SharingLet’s walk through how we would use Shamir’s secret sharing to construct a (2, n) secret sharing scheme.Suppose we have secret k to distribute into n shares, s_1,…, s_n, among n parties, P_1,…, P_n.In a (2, n) scheme, any 2 points should uniquely define the polynomial p used for computing the shares.So, we’ll generate a random degree 1 polynomial (i.e. a straight line), such that p(0) = k. Specifically, let’s define p(x) = a*x + k, where a ∈ ℕ.Compute n shares s_1,…, s_n, such that s_i = p(i) = a*i + k, ∀i={1,…, n}.Distribute share s_i to party P_i, ∀i={1,…, n}.Note: in practice, the protocol requires establishing some large prime number g, over which all coefficients and computations are to be completed within the finite field defined by g. However, omitting that detail doesn’t change the intuition/major steps of the protocol.Shamir’s (2, 3) secret sharing. Image by authorIs this (2, n) secret sharing scheme correct? Can we pick any pair of shares to derive k?Consider parties P_i, P_j, with shares s_i = a*i + k, s_j = a*j + k, respectively.We can represent this pooled information as a system of equations with 2 equations, 2 unknowns.Image by authorNotice that A (defined above) is a 2 x 2 Vandermonde matrix such that det(A) = j — i ≠ 0, i.e. A is invertible.Thus, we may derive the polynomial by multiplying the inverse of A to both sides, recovering secret k in the process.Image by authorIs this (2, n) secret sharing scheme secure? That is, no single share provides sufficient information to derive k?Let’s consider the viewpoint of a single party P_i in this protocol.P_i knows their own share s_i = a*i + k. Since no other parties are pooling shares, P_i has no knowledge about the other shares s_j, ∀j ≠ i.Recall: a is some random non-zero integer. Therefore, a*i is also indistinguishable from some random non-zero integer.Thus, s_i = a*i + k is the sum of some number k with some number, a*i, which is indistinguishable from random. So, it follows that s_i is also indistinguishable from random, thus revealing no intelligible information about k.Extending to (t, n)Let’s extend the example above to construct a (t, n) secret sharing scheme.The steps are the same as the (2, n) example above, the only difference being that the polynomial we use to define the shares must be uniquely defined by any t points.Thus, let’s generate a random degree t-1 polynomial, p, such that p(0) = k. Specifically, define p(x) = a_{t-1}*x^{t-1} +…+ a_1*x + k, where a_i ∈ ℤ, and a_{t-1} ≠ 0.Define P_i’s share, s_i, such that s_i = p(i) = a_{t-1}*i^{t-1} +…+ a_1*i + k, ∀ i={1,…, n}.Let’s examine the correctness of this (t, n) scheme. Does any subset of t shares provide sufficient information to derive secret k?Consider parties P_1,…,P_t who wish to pool their shares s_1,…, s_t to derive k.We can represent this information with the following system of t equations, t unknowns.Image by authorA is a t x t Vandermonde matrix such that det(A) = Π(s_j — s_i), ∀i ≠ j. It turns out that this sequential product is non-zero, i.e. A is invertible. Check this out if you’re interested in the proof behind the non-zero determinant of any square Vandermonde matrix.Thus, we can multiply both sides by the inverse of A and solve the system below to derive polynomial p and secret k.Image by authorLet’s examine the security of this (t, n) scheme. Does it hold that no subset of t-1 shares provides sufficient information to derive secret k?Consider t-1 parties P_1,…,P_{t-1} who wish to pool their shares s_1,…, s_{t-1}.We can represent this information with the following system of equations:Image by authorNotice the system above contains t-1 equations and t unknown parameters.Therefore, we can vary one of these parameters (secret k) freely while still satisfying the point constraints s_1,…, s_{t-1}. In other words, any value of k ∈ ℝ is equally likely to be the intercept of a polynomial that contains those shares s_1,…, s_{t-1}.Properties of Shamir’s Secret SharingThe examples above illustrated how Shamir’s secret sharing is information-theoretically secure i.e. no subset of parties smaller than the established threshold, t, may derive any intelligible information about k. Let’s look at some additional properties of Shamir’s secret sharing.Once a (t, n) secret sharing scheme is established, it may be easily extended to additional parties.If new parties want to participate in the secret sharing scheme, we can simply generate new shares by evaluating more points on the defining polynomial ex: s_{i+1} = p(i+1), s_{i+2} = p(i+2), etc.This changes nothing about the security guarantees of the secret sharing scheme, as the degree of the defining polynomial remains the same.However, once a share is established for a participating party, there is no way to “invalidate” their share from the pool of other shares.Consider some organization A, who has some secret information, k, split among members internal to the organization via Shamir’s (t, n) secret sharing.If any subset of these t members leaves the organization, they may pool their shares to derive k, leaking k external to the organization.Preventing this would require re-executing the Shamir protocol periodically to define a new random polynomial for recomputing shares and redistributing them to the relevant parties.For more information about properties/consequences of Shamir’s secret sharing, I highly recommend this read.Implementation in CodeBelow is a basic python implementation of Shamir’s (t, n) secret sharing as we discussed here. All the relevant methods implementing the algorithmic logic behind Shamir’s secret sharing are included below. Some unrelated utility functions are omitted to keep it concise.Feel free to check out the Github below.GitHub – jimin-kang/Shamir-Secret-Sharingimport random # in practice, this should be cryptographically secureimport numpy as npfrom numpy.polynomial import polynomial as Pfrom prompt_inputs import accept_scheme_parameters, prompt_pooled_parties# prime number to define the finite field where coefficients will be sampled from# in practice, FIELD_SIZE > max(n, k) FIELD_SIZE = 65521def generate_polynomial(d, k): “”” Parameters: d: degree of polynomial to be generated k: secret to define polynomial y-intercept Returns: poly: vector of polynomial coefficients & intercept ordered from intercept term to largest degree term i.e. [k, a_{1}, a_{2},…, a_{t-1}] “”” # generate random coeffcients from {0,…,p-1} poly = [random.randint(0, FIELD_SIZE-1) for _ in range(d)] # coefficient of largest degree term must be non-zero poly[-1] = random.randint(1, FIELD_SIZE-1) # place secret at y-intercept i.e. p(0) = k poly.insert(0, k) return polydef compute_shares(poly, n): “”” Parameters: coeff: polynomial coefficients ordered from intercept term to largest degree term i.e. [k, a_{1}, a_{2},…, a_{t-1}] n: number of parties to distribute secret shares to Returns: shares: vector of computed shares ordered by ascending order of party index i.e. [s_{1}, s_{2},…, s_{n}] “”” # evaluate polynomial at x in {1, 2,…, n} x = np.arange(1, n + 1, 1) # Generate the Vandermonde matrix vandermonde = P.polyvander(x=x, deg=len(poly)-1) # shares = vandermonde * poly shares = vandermonde @ poly return sharesdef reconstruct_secret(shares, indices): “”” Parameters: shares: pooled share values indices: parties corresponding to pooled share values Returns: secret & vector containing polynomial coefficients and secret “”” # Vandermonde matrix for pooled parties vandermonde = P.polyvander(x=indices, deg=len(indices)-1) # coeff = inv(Vandermonde) * shares poly = np.linalg.inv(vandermonde) @ np.array(shares) # rounding to deal w/ floating pt. precision errors: wrapping integer lists into numpy arrays may promote integers into floats # polynomial coefficients are integers in {0,…,p-1} poly = [float(poly[0])] + [round(x) for x in poly[1:]] print(f”Reconstructed Secret: {poly[0]}”) print(f”Reconstructed Polynomial: {poly}”)def display_scheme_info(k, poly, shares): “”” Display secret (k), polynomial, and shares for the participating parties in the (t, n) secret sharing scheme. “”” print(f”Secret: {k}”) print(f”Polynomial: {poly}”) print(“Shares:”) for i, share in enumerate(shares): print(f” Party {i+1}: {share}”)def main(): # define scheme & compute/distribute shares t, n, k = accept_scheme_parameters() poly = generate_polynomial(t-1, k) shares = compute_shares(poly, n) display_scheme_info(k, poly, shares) # prompt for shares to pool pooled_parties = prompt_pooled_parties(t, n) pooled_shares = [shares[i-1] for i in pooled_parties] # reconstruct secret from pooled shares reconstruct_secret(pooled_shares, pooled_parties) Wrap-upThanks for reading! A brief recap about what we talked about:Secret sharing is a method for parties to distribute some secret information among themselves such that any sufficiently large subset of parties may recover the secret, but no smaller subset may derive any intelligible information about the secret.Shamir’s secret sharing scheme is a specific secret sharing algorithm that is information theoretically secure. The scheme uses random polynomials to compute secret shares and invertible matrices to recover the secret.Shamir’s secret sharing scheme is one that nearly always comes up in any discussion about secret sharing due to its efficiency and unconditional security, but other efficient secret sharing algorithms are used in practice as well. For more information about other secret sharing algorithms, or if you’d like to explore Shamir’s secret sharing at a deeper level, check out the resources below!SourcesSecret sharing)MIT 6.875 (Fall 2023)GeeksForGeeks, Additive Secret SharingFarid Hajji, How to Share a SecretAdi Shamir, How to Share a SecretWikipedia, Secret SharingVandermonde matrix)Wikipedia, Vandermonde MatrixMathematics Stack Exchange, Find N degree polynomial from N+1 pointsMathematics Stack Exchange, Vandermonde determinant by inductionApplications to privacy-preserving data science)Ghavamipour, A.R., Turkmen, F. & Jiang, X. Privacy-preserving logistic regression with secret sharing. BMC Med Inform Decis Mak 22, 89 (2022)Jia Duan, Jiantao Zhou, Yuanman Li,Privacy-Preserving distributed deep learning based on secret sharing,Information Sciences, Volume 527, 2020, Pages 108–127How to Share a Secret: Shamir’s Secret Sharing was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.  privacy, multi-party-computation, data-privacy, cryptography, secret-sharing Towards Data Science – MediumRead More

Add to favorites