DISCLAIMER: This is not financial advice. I’m a PhD in Aerospace Engineering with a strong focus on Machine Learning: I’m not a financial advisor. This article is intended solely to demonstrate the power of Physics-Informed Neural Networks (PINNs) in a financial context.
When I was 16, I fell in love with Physics. The reason was simple yet powerful: I thought Physics was fair.
It never happened that I got an exercise wrong because the speed of light changed overnight, or because suddenly ex could be negative. Every time I read a physics paper and thought, “This doesn’t make sense,” it turned out I was the one not making sense.
So, Physics is always fair, and because of that, it’s always perfect. And Physics displays this perfection and fairness through its set of rules, which are known as differential equations.
The simplest differential equation I know is this one:

Very simple: we start here, x0=0, at time t=0, then we move with a constant speed of 5 m/s. This means that after 1 second, we are 5 meters (or miles, if you like it best) away from the origin; after 2 seconds, we are 10 meters away from the origin; after 43128 seconds… I think you got it.
As we were saying, this is written in stone: perfect, ideal, and unquestionable. Nonetheless, imagine this in real life. Imagine you are out for a walk or driving. Even if you try your best to go at a target speed, you will never be able to keep it constant. Your mind will race in certain parts; maybe you will get distracted, maybe you will stop for red lights, most likely a combination of the above. So maybe the simple differential equation we mentioned earlier is not enough. What we could do is to try and predict your location from the differential equation, but with the help of Artificial Intelligence.
This idea is implemented in Physics Informed Neural Networks (PINN). We will describe them later in detail, but the idea is that we try to match both the data and what we know from the differential equation that describes the phenomenon. This means that we enforce our solution to generally meet what we expect from Physics. I know it sounds like black magic, I promise it will be clearer throughout the post.
Now, the big question:
What does Finance have to do with Physics and Physics Informed Neural Networks?
Well, it turns out that differential equations are not only useful for nerds like me who are interested in the laws of the natural universe, but they can be useful in financial models as well. For example, the Black-Scholes model uses a differential equation to set the price of a call option to have, given certain quite strict assumptions, a risk-free portfolio.
The goal of this very convoluted introduction was twofold:
- Confuse you just a little, so that you will keep reading

- Spark your curiosity just enough to see where this is all going.
Hopefully I managed  . If I did, the rest of the article would follow these steps:
. If I did, the rest of the article would follow these steps:
- We will discuss the Black-Scholes model, its assumptions, and its differential equation
- We will talk about Physics Informed Neural Networks (PINNs), where they come from, and why they are helpful
- We will develop our algorithm that trains a PINN on Black-Scholes using Python, Torch, and OOP.
- We will show the results of our algorithm.
I’m excited! To the lab! 
1. Black Scholes Model
If you are curious about the original paper of Black-Scholes, you can find it here. It’s definitely worth it
Ok, so now we have to understand the Finance universe we are in, what the variables are, and what the laws are.
First off, in Finance, there is a powerful tool called a call option. The call option gives you the right (not the obligation) to buy a stock at a certain price in the fixed future (let’s say a year from now), which is called the strike price.
Now let’s think about it for a moment, shall we? Let’s say that today the given stock price is $100. Let us also assume that we hold a call option with a $100 strike price. Now let’s say that in one year the stock price goes to $150. That’s amazing! We can use that call option to buy the stock and then immediately resell it! We just made $150 – $150-$100 = $50 profit. On the other hand, if in one year the stock price goes down to $80, then we can’t do that. Actually, we are better off not exercising our right to buy at all, not to lose money.
So now that we think about it, the idea of buying a stock and selling an option turns out to be perfectly complementary. What I mean is the randomness of the stock price (the fact that it goes up and down) can actually be mitigated by holding the right number of options. This is called delta hedging.
Based on a set of assumptions, we can derive the fair option price in order to have a risk-free portfolio.
I don’t want to bore you with all the details of the derivation (they are honestly not that hard to follow in the original paper), but the differential equation of the risk-free portfolio is this:

Where:
Cis the price of the option at time tsigmais the volatility of the stockris the risk-free ratetis time (with t=0 now and T at expiration)Sis the current stock price
From this equation, we can derive the fair price of the call option to have a risk-free portfolio. The equation is closed and analytical, and it looks like this:

With:

Where N(x) is the cumulative distribution function (CDF) of the standard normal distribution, K is the strike price, and T is the expiration time.
For example, this is the plot of the Stock Price (x) vs Call Option (y), according to the Black-Scholes model.

Now this looks cool and all, but what does it have to do with Physics and PINN? It looks like the equation is analytical, so why PINN? Why AI? Why am I reading this at all? The answer is below  :
:
2. Physics Informed Neural Networks
If you are curious about Physics Informed Neural Networks, you can find out in the original paper here. Again, worth a read.

Now, the equation above is analytical, but again, that is an equation of a fair price in an ideal scenario. What happens if we ignore this for a moment and try to guess the price of the option given the stock price and the time? For example, we could use a Feed Forward Neural Network and train it through backpropagation.
In this training mechanism, we are minimizing the error
L = |Estimated C - Real C|:

This is fine, and it is the simplest Neural Network approach you could do. The issue here is that we are completely ignoring the Black-Scholes equation. So, is there another way? Can we possibly integrate it?
Of course, we can, that is, if we set the error to be
L = |Estimated C - Real C|+ PDE(C,S,t)
Where PDE(C,S,t) is

And it needs to be as close to 0 as possible:

But the question still stands. Why is this “better” than the simple Black-Scholes? Why not just use the differential equation? Well, because sometimes, in life, solving the differential equation doesn’t guarantee you the “real” solution. Physics is usually approximating things, and it is doing that in a way that could create a difference between what we expect and what we see. That is why the PINN is an amazing and fascinating tool: you try to match the physics, but you are strict in the fact that the results have to match what you “see” from your dataset.
In our case, it might be that, in order to obtain a risk-free portfolio, we find that the theoretical Black-Scholes model doesn’t fully match the noisy, biased, or imperfect market data we’re observing. Maybe the volatility isn’t constant. Maybe the market isn’t efficient. Maybe the assumptions behind the equation just don’t hold up. That is where an approach like PINN can be helpful. We not only find a solution that meets the Black-Scholes equation, but we also “trust” what we see from the data.
Ok, enough with the theory. Let’s code. 
3. Hands On Python Implementation
The whole code, with a cool README.md, a fantastic notebook and a super clear modular code, can be found here
P.S. This will be a little intense (a lot of code), and if you are not into software, feel free to skip to the next chapter. I will show the results in a more friendly way
Thank you a lot for getting to this point 
Let’s see how we can implement this.
3.1 Config.json file
The whole code can run with a very simple configuration file, which I called config.json.
You can place it wherever you like, as we will see.
This file is crucial, as it defines all the parameters that govern our simulation, data generation, and model training. Let me quickly walk you through what each value represents:
K: the strike price — this is the price at which the option gives you the right to buy the stock in the future.T: the time to maturity, in years. SoT = 1.0means the option expires one unit (for example, one year) from now.r: the risk-free interest rate is used to discount future values. This is the interest rate we are setting in our simulation.sigma: the volatility of the stock, which quantifies how unpredictable or “risky” the stock price is. Again, a simulation parameter.N_data: the number of synthetic data points we want to generate for training. This will condition the size of the model as well.min_Sandmax_S: the range of stock prices we want to sample when generating synthetic data. Min and max in our stock price.bias: an optional offset added to the option prices, to simulate a systemic shift in the data. This is done to create a discrepancy between the real world and the Black-Scholes datanoise_variance: the amount of noise added to the option prices to simulate measurement or market noise. This parameter is add for the same reason as before.epochs: how many iterations the model will train for.lr: the learning rate of the optimizer. This controls how fast the model updates during training.log_interval: how often (in terms of epochs) we want to print logs to monitor training progress.
Each of these parameters plays a specific role, some shape the financial world we’re simulating, others control how our neural network interacts with that world. Small tweaks here can lead to very different behavior, which makes this file both powerful and delicate. Changing the values of this JSON file will radically change the output of the code.
3.2 main.py
Now let’s look at how the rest of the code uses this config in practice.
The main part of our code comes from main.py, train your PINN using Torch, and black_scholes.py.
This is main.py:
So what you can do is:
- Build your config.json file
- Run
python main.py --config config.json
main.py uses a lot of other files.
3.3 black_scholes.py and helpers
The implementation of the model is inside black_scholes.py:
This can be used to build the model, train, export, and predict.
The function uses some helpers as well, like data.py, loss.py, and model.py.
The torch model is inside model.py:
The data builder (given the config file) is inside data.py:
And the beautiful loss function that incorporates the value of is loss.py
4. Results
Ok, so if we run main.py, our FFNN gets trained, and we get this.

As you notice, the model error is not quite 0, but the PDE of the model is much smaller than the data. That means that the model is (naturally) aggressively forcing our predictions to meet the differential equations. This is exactly what we said before: we optimize both in terms of the data that we have and in terms of the Black-Scholes model.
We can notice, qualitatively, that there is a great match between the noisy + biased real-world (rather realistic-world lol) dataset and the PINN.

These are the results when t = 0, and the Stock price changes with the Call Option at a fixed t. Pretty cool, right? But it’s not over! You can explore the results using the code above in two ways:
- Playing with the multitude of parameters that you have in config.json
- Seeing the predictions at t>0
Have fun! 
5. Conclusions
Thank you so much for making it all the way through. Seriously, this was a long one 
Here’s what you’ve seen in this article:
- We started with Physics, and how its rules, written as differential equations, are fair, beautiful, and (usually) predictable.
- We jumped into Finance, and met the Black-Scholes model — a differential equation that aims to price options in a risk-free way.
- We explored Physics-Informed Neural Networks (PINNs), a type of neural network that doesn’t just fit data but respects the underlying differential equation.
- We implemented everything in Python, using PyTorch and a clean, modular codebase that lets you tweak parameters, generate synthetic data, and train your own PINNs to solve Black-Scholes.
- We visualized the results and saw how the network learned to match not only the noisy data but also the behavior expected by the Black-Scholes equation.
Now, I know that digesting all of this at once is not easy. In some areas, I was necessarily short, maybe shorter than I needed to be. Nonetheless, if you want to see things in a clearer way, again, give a look at the GitHub folder. Even if you are not into software, there is a clear README.md and a simple example/BlackScholesModel.ipynb that explains the project step by step.
6. About me!
Thank you again for your time. It means a lot 
My name is Piero Paialunga, and I’m this guy here:

I am a Ph.D. candidate at the University of Cincinnati Aerospace Engineering Department. I talk about AI, and Machine Learning in my blog posts and on LinkedIn and here on TDS. If you liked the article and want to know more about machine learning and follow my studies you can:
A. Follow me on Linkedin, where I publish all my stories
B. Follow me on GitHub, where you can see all my code
C. Send me an email: [email protected]
D. Want to work with me? Check my rates and projects on Upwork!
Ciao. 
P.S. My PhD is ending and I’m considering my next step for my career! If you like how I work and you want to hire me, don’t hesitate to reach out.

The post When Physics Meets Finance: Using AI to Solve Black-Scholes appeared first on Towards Data Science.
Here’s how to use Physics-Informed Neural Networks to solve Financial Models, with Python.
The post When Physics Meets Finance: Using AI to Solve Black-Scholes appeared first on Towards Data Science. Artificial Intelligence, Deep Learning, Finance, Machine Learning, Python Towards Data ScienceRead More

 Add to favorites
Add to favorites

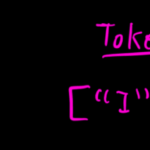
0 Comments