Introduction

The Attention Mechanism is often associated with the transformer architecture, but it was already used in RNNs. In Machine Translation or MT (e.g., English-Italian) tasks, when you want to predict the next Italian word, you need your model to focus, or pay attention, on the most important English words that are useful to make a good translation.

I will not go into details of RNNs, but attention helped these models to mitigate the vanishing gradient problem and to capture more long-range dependencies among words.

At a certain point, we understood that the only important thing was the attention mechanism, and the entire RNN architecture was overkill. Hence, Attention is All You Need!

Self-Attention in Transformers

Classical attention indicates where words in the output sequence should focus attention in relation to the words in input sequence. This is important in sequence-to-sequence tasks like MT.

The self-attention is a specific type of attention. It operates between any two elements in the same sequence. It provides information on how “correlated” the words are in the same sentence.

For a given token (or word) in a sequence, self-attention generates a list of attention weights corresponding to all other tokens in the sequence. This process is applied to each token in the sentence, obtaining a matrix of attention weights (as in the picture).

This is the general idea, in practice things are a bit more complicated because we want to add many learnable parameters to our neural network, let’s see how.

K, V, Q representations

Our model input is a sentence like “my name is Marcello Politi”. With the process of tokenization, a sentence is converted into a list of numbers like [2, 6, 8, 3, 1].

Before feeding the sentence into the transformer we need to create a dense representation for each token.

How to create this representation? We multiply each token by a matrix. The matrix is learned during training.

Let’s add some complexity now.

For each token, we create 3 vectors instead of one, we call these vectors: key, value and query. (We see later how we create these 3 vectors).

Conceptually these 3 tokens have a particular meaning:

• The vector key represents the core information captured by the token
• The vector value captures the full information of a token
• The vector query, it’s a question about the token relevance for the current task.

So the idea is that we focus on a particular token i , and we want to ask what is the importance of the other tokens in the sentence regarding the token i we are taking into consideration.

This means that we take the vector q_i (we ask a question regarding i) for token i, and we do some mathematical operations with all the other tokens k_j (j!=i). This is like wondering at first glance what are the other tokens in the sequence that look really important to understand the meaning of token i.

What is this magical mathematical operation?

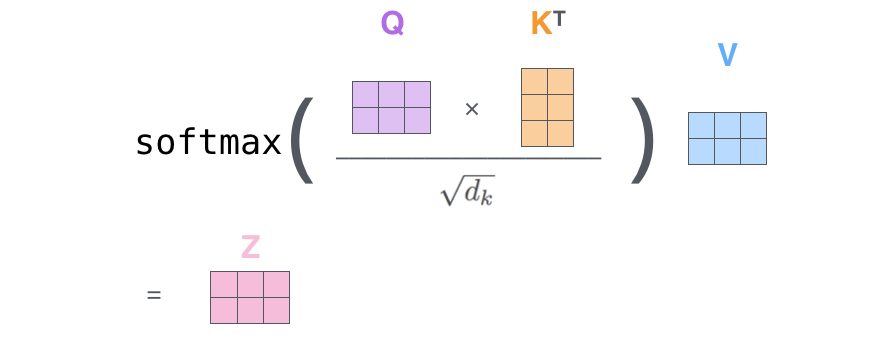
We need to multiply (dot-product) the query vector by the key vectors and divide by a scaling factor. We do this for each k_j token.

In this way, we obtain a score for each pair (q_i, k_j). We make this list become a probability distribution by applying a softmax operation on it. Great now we have obtained the attention weights!

With the attention weights, we know what is the importance of each token k_j to for undestandin the token i. So now we multiply the value vector v_j associated with each token per its weight and we sum the vectors. In this way we obtain the final context-aware vector of token_i.

If we are computing the contextual dense vector of token_1 we calculate:

z1 = a11*v1 + a12*v2 + … + a15*v5

Where a1j are the computer attention weights, and v_j are the value vectors.

Done! Almost…

I didn’t cover how we obtained the vectors k, v and q of each token. We need to define some matrices w_k, w_v and w_q so that when we multiply:

• token * w_k -> k
• token * w_q -> q
• token * w_v -> v

These 3 matrices are set at random and are learned during training, this is why we have many parameters in modern models such as LLMs.

Multi-head Self-Attention in Transformers (MHSA)

Are we sure that the previous self-attention mechanism is able to capture all important relationships among tokens (words) and create dense vectors of those tokens that really make sense?

It could actually not work always perfectly. What if to mitigate the error we re-run the entire thing 2 times with new w_q, w_k and w_v matrices and somehow merge the 2 dense vectors obtained? In this way maybe one self-attention managed to capture some relationship and the other managed to capture some other relationship.

Well, this is what exactly happens in MHSA. The case we just discussed contains two heads because it has two sets of w_q, w_k and w_v matrices. We can have even more heads: 4, 8, 16 etc.

The only complicated thing is that all these heads are managed in parallel, we process the all in the same computation using tensors.

The way we merge the dense vectors of each head is simple, we concatenate them (hence the dimension of each vector shall be smaller so that when concat them we obtain the original dimension we wanted), and we pass the obtained vector through another w_o learnable matrix.

Hands-on

Python">import torch

Suppose you have a sentence. After tokenization, each token (word for simplicity) corresponds to an index (number):

tokenized_sentence = torch.tensor([
    2, #my
    6, #name
    8, #is
    3, #marcello
    1  #politi
])
tokenized_sentence

Before feeding the sentence into the transofrmer we need to create a dense representation for each token.

How to create these representation? We multiply each token per a matrix. This matrix is learned during training.

Let’s build this embedding matrix.

torch.manual_seed(0) # set a fixed seed for reproducibility
embed = torch.nn.Embedding(10, 16)

If we multiply our tokenized sentence with the embeddings, we obtain a dense representation of dimension 16 for each token

sentence_embed = embed(tokenized_sentence).detach()
sentence_embed

In order to use the attention mechanism we need to create 3 new We define 3 matrixes w_q, w_k and w_v. When we multiply one input token time the w_q we obtain the vector q. Same with w_k and w_v.

d = sentence_embed.shape[1] # let's base our matrix on a shape (16,16)

w_key = torch.rand(d,d)
w_query = torch.rand(d,d)
w_value = torch.rand(d,d)

Compute attention weights

Let’s now compute the attention weights for only the first input token of the sentence.

token1_embed = sentence_embed[0]

#compute the tre vector associated to token1 vector : q,k,v
key_1 = w_key.matmul(token1_embed)
query_1 = w_query.matmul(token1_embed)
value_1 = w_value.matmul(token1_embed)

print("key vector for token1: n", key_1)   
print("query vector for token1: n", query_1)
print("value vector for token1: n", value_1)

We need to multiply the query vector associated to token1 (query_1) with all the keys of the other vectors.

So now we need to compute all the keys (key_2, key_2, key_4, key_5). But wait, we can compute all of these in one time by multiplying the sentence_embed times the w_k matrix.

keys = sentence_embed.matmul(w_key.T)
keys[0] #contains the key vector of the first token and so on

Let’s do the same thing with the values

values = sentence_embed.matmul(w_value.T)
values[0] #contains the value vector of the first token and so on

Let’s compute the first part of the attions formula.

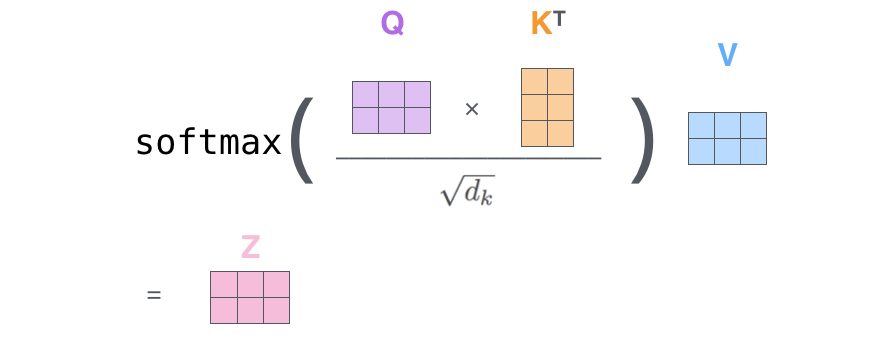
import torch.nn.functional as F

# the following are the attention weights of the first tokens to all the others
a1 = F.softmax(query_1.matmul(keys.T)/d**0.5, dim = 0)
a1

With the attention weights we know what is the importance of each token. So now we multiply the value vector associated to each token per its weight.

To obtain the final context aware vector of token_1.

z1 = a1.matmul(values)
z1

In the same way we could compute the context aware dense vectors of all the other tokens. Now we are always using the same matrices w_k, w_q, w_v. We say that we use one head.

But we can have multiple triplets of matrices, so multi-head. That’s why it is called multi-head attention.

The dense vectors of an input tokens, given in oputut from each head are at then end concatenated and linearly transformed to get the final dense vector.

Implementing MultiheadSelf-Attention

import torch
import torch.nn as nn
import torch.nn.functional as F

torch.manual_seed(0) # fixed seed for reproducibility

Same steps as before…

# Tokenized sentence (same as yours)
tokenized_sentence = torch.tensor([2, 6, 8, 3, 1])  # [my, name, is, marcello, politi]

# Embedding layer: vocab size = 10, embedding dim = 16
embed = nn.Embedding(10, 16)
sentence_embed = embed(tokenized_sentence).detach()  # Shape: [5, 16] (seq_len, embed_dim)

We’ll define a multi-head attention mechanism with h heads (let’s say 4 heads for this example). Each head will have its own w_q, w_k, and w_v matrices, and the output of each head will be concatenated and passed through a final linear layer.

Since the output of the head will be concatenated, and we want a final dimension of d, the dimension of each head needs to be d/h. Additionally each concatenated vector will go though a linear transformation, so we need another matrix w_ouptut as you can see in the formula.

d = sentence_embed.shape[1]  # embed dimension 16
h = 4  # Number of heads
d_k = d // h  # Dimension per head (16 / 4 = 4)

Since we have 4 heads, we want 4 copies for each matrix. Instead of copies, we add a dimension, which is the same thing, but we only do one operation. (Imagine stacking matrices on top of each other, its the same thing).

# Define weight matrices for each head
w_query = torch.rand(h, d, d_k)  # Shape: [4, 16, 4] (one d x d_k matrix per head)
w_key = torch.rand(h, d, d_k)    # Shape: [4, 16, 4]
w_value = torch.rand(h, d, d_k)  # Shape: [4, 16, 4]
w_output = torch.rand(d, d)  # Final linear layer: [16, 16]

I’m using for simplicity torch’s einsum. If you’re not familiar with it check out my blog post.

The einsum operation torch.einsum('sd,hde->hse', sentence_embed, w_query) in PyTorch uses letters to define how to multiply and rearrange numbers. Here’s what each part means:

1. Input Tensors:
   • sentence_embed with the notation 'sd':
     • s represents the number of words (sequence length), which is 5.
     • d represents the number of numbers per word (embedding size), which is 16.
     • The shape of this tensor is [5, 16].
   • w_query with the notation 'hde':
     • h represents the number of heads, which is 4.
     • d represents the embedding size, which again is 16.
     • e represents the new number size per head (d_k), which is 4.
     • The shape of this tensor is [4, 16, 4].
2. Output Tensor:
   • The output has the notation 'hse':
     • h represents 4 heads.
     • s represents 5 words.
     • e represents 4 numbers per head.
     • The shape of the output tensor is [4, 5, 4].

# Compute Q, K, V for all tokens and all heads
# sentence_embed: [5, 16] -> Q: [4, 5, 4] (h, seq_len, d_k)
queries = torch.einsum('sd,hde->hse', sentence_embed, w_query)  # h heads, seq_len tokens, d dim
keys = torch.einsum('sd,hde->hse', sentence_embed, w_key)       # h heads, seq_len tokens, d dim
values = torch.einsum('sd,hde->hse', sentence_embed, w_value)   # h heads, seq_len tokens, d dim

This einsum equation performs a dot product between the queries (hse) and the transposed keys (hek) to obtain scores of shape [h, seq_len, seq_len], where:

• h -> Number of heads.
• s and k -> Sequence length (number of tokens).
• e -> Dimension of each head (d_k).

The division by (d_k ** 0.5) scales the scores to stabilize gradients. Softmax is then applied to obtain attention weights:

# Compute attention scores
scores = torch.einsum('hse,hek->hsk', queries, keys.transpose(-2, -1)) / (d_k ** 0.5)  # [4, 5, 5]
attention_weights = F.softmax(scores, dim=-1)  # [4, 5, 5]

# Apply attention weights
head_outputs = torch.einsum('hij,hjk->hik', attention_weights, values)  # [4, 5, 4]
head_outputs.shape

Now we concatenate all the heads of token 1

# Concatenate heads
concat_heads = head_outputs.permute(1, 0, 2).reshape(sentence_embed.shape[0], -1)  # [5, 16]
concat_heads.shape

Let’s finally multiply per the last w_output matrix as in the formula above

multihead_output = concat_heads.matmul(w_output)  # [5, 16] @ [16, 16] -> [5, 16]
print("Multi-head attention output for token1:n", multihead_output[0])

Final Thoughts

In this blog post I’ve implemented a simple version of the attention mechanism. This is not how it is really implemented in modern frameworks, but my scope is to provide some insights to allow anyone an understanding of how this works. In future articles I’ll go through the entire implementation of a transformer architecture.

Follow me on TDS if you like this article!

 Linkedin |  X (Twitter) |  Website

---

Unless otherwise noted, images are by the author

The post A Simple Implementation of the Attention Mechanism from Scratch appeared first on Towards Data Science.

​How attention helped models like RNNs mitigate the vanishing gradient problem and capture long-range dependencies among words
The post A Simple Implementation of the Attention Mechanism from Scratch appeared first on Towards Data Science.  Artificial Intelligence, Machine Learning, Attention Mechanism, Deep Learning, Python, Self Attention Towards Data ScienceRead More

Add to favorites