When A/B Tests Are Not The Right Choice

Bandit Algorithm Or A/B Test?

Imagine working as a Data Scientist for an adtech company and you are serving ads on behalf of a client. If that client comes to you and says that they have 2 variants in mind (i.e. changes to creative / message / offer ) for their upcoming campaign and they want to figure out “which ad is best”, what do you do? Run an A/B test where you randomly split the targeting units (people, devices, geographies) in half and serve one variant in each sample, let the campaign run and measure which ad produced the best result? Sounds reasonable!

What if the client comes to you and says they have 25 ad variants in mind? Even at “adtech scale”, will there be enough measurable [clicks / visits / purchases] to support sufficient statistical power for the experiment?

What if the client tells you that this campaign is not a recurring one where the knowledge gained for which ad is best, will be useful for the next campaign but instead that it is supporting a special event or one-off and wont be repeated (soon)? Does that change things?

Standard statistical testing frameworks which we may position under the umbrella of A/B testing has its place and is rightfully popular in industry. There are cases where it completely breaks down though — as hinted at above. It can become infeasible to gather sufficient data during the course of an experiment to satisfy the demands of statistical power for rigorous experiments when there are more than a few treatments involved. Further, the premise of an A/B test is to devise treatment selection for future campaigns based on the results of past campaigns. If this isn’t an option — imagine a campaign for the launch of a new product or a seasonal event that wont be repeated for a year — while there may be some learning that can transfer, its unlikely that determining the exact best creative this time will be relevant next time. Plus, there is an opportunity cost involved with A/B tests. In order to measure all the variants involved, there will be a significant portion of the budget dedicated to low(er) performing ads over the duration of the campaign.

In these situations, instead of an A/B test, a bandit algorithm can be utilized. In this case, we are less interested in high statistical confidence around the each treatment effect but we want to focus as much of the budget towards what we think seems like the best performing variant during the campaign.

The basic idea of a bandit algorithm is that we learn a policy which maximizes the reward of the environment. In terms of our marketing example, this means we want to serve the ad variant which produces the highest KPI (e.g. click through rate) in the campaign (e.g. an online ad serving environment).

Explaining bandit algorithms like multi-arm bandits is outside of the scope of this post, but at a high level, the key components are as follows:

Arms

• Each arm (e.g. ad variant) represents an option to choose.
• Each arm has an unknown reward distribution and the goal is to find the best arm over time.

Rewards

• Each time an arm is pulled (e.g. ad served), it provides a reward (click or no click) from an unknown probability distribution.
• The objective is to maximize the total rewards.

Policy

• A policy is the strategy (i.e. model or rule) followed to decide which arm to pull at each opportunity.

Exploration vs. Exploitation Trade-off

• Exploration: Trying different arms to gather more information about their rewards.
• Exploitation: Selecting the arm that has provided the highest reward so far to maximize gains.

The basic multi-arm bandit (MAB) algorithm (e.g. Thompson Sampling) seeks to find the best marginal arm. The goal in our scenario is to find the ad variant that produces the highest KPI for the entire population. Contextual Multi-arm bandits (CMAB) on the other hand, take this a step further and recognize that some arms may produce higher rewards with some segments of the population than others. Hence in marketing, we can personalize the ad being served.

Environment Simulation

If the campaign is evergreen and we have no past results, we can simulate the outcomes and measure how well various algorithms work and debug our serving code. This is much easier in terms of an MAB than the contextual side. Now, if we happen to have access to logged data from a prior campaign where the arms were selected based on an existing policy, we can use that data to compare a new algorithm to an existing one.

Another way we can explore the workings of a bandit algorithm and compare performance between optional implementations is through simulation, but instead of building this from scratch, we can instead repurpose any multiclass or multi-label dataset used for supervised learning.

For this environment simulation, we will borrow heavily (with some changes) from an excellent example in Enes Bilgin’s Mastering Reinforcement Learning with Python. Lets walk through the situation and environment components piece by piece.

Data

The environment will leverage an common dataset used for ML benchmarking and illustrates how a typical dataset used for classification and regression problems can be repurposed to be used by a CB application. The one chosen comes from the 1994 census and contains 32,561 rows and we will use 11 columns. A sample of the data follows, where we pay special attention to the Education column.

There are 16 distinct levels of education ranging from “Preschool” to “Doctorate”

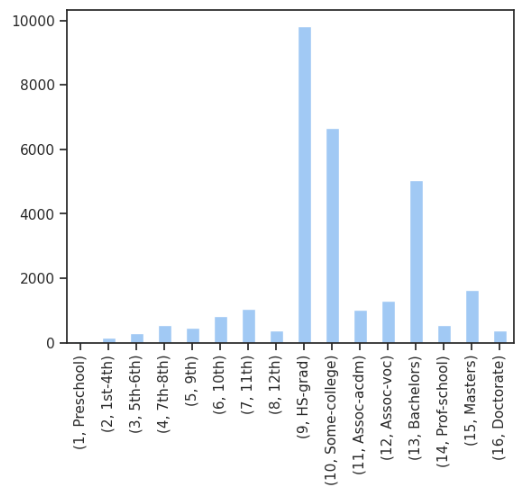
Our first environmental function simply samples the dataset and returns a single observation. We then separate out the education value from the rest of the columns, which we call “context”.

def generate_user(df_data):
    user = df_data.sample(1)   # everything 
    
    ed = user['education']
    context = user.drop('education', axis =1)
    context = context.values.tolist()[0] # all but education
    return ed.values.tolist()[0], context

Setup

At this point we need to explain the setup of the simulation. We are simulating an online advertising environment where users come to the application one at at time. In reality there is not an orderly queue of course but this doesn’t impact the generality of the simulation.

We understand the context to contain information about the user, the specific state of the application, the time of day of the visit and other data. In our case the context is expressed through the 10 features in our dataset. These elements are all known and visible upon their arrival. The education level of the user is not known and is hidden from the policy. Our desire is to serve one of sixteen ads we have available, to the user in the hopes that they click on the ad.

The education feature represents both a key aspect of the user and the available ads.

Applicable Ads

At any point where we have an opportunity to serve an ad, not all ads are possible. We are adding this complexity to simulate a common occurrence where depending on the context (e.g. the web page or some user characteristic) not all available ads are appropriate.

We accomplish this with a simple function where the available ads each have a fixed probability of being appropriate for the context. This is a simple uniform probability where each ad is randomly and independently included or excluded from the available inventory.

def get_ad_inventory(prob = 0.8):
    ad_inventory = []
    for level in available_ads:
        if U() < prob: # uniform prob U
            ad_inventory.append(level)
    # Make sure there are at least one ad
    if not ad_inventory:
        ad_inventory = get_ad_inventory()
    return ad_inventory

Reward

For each opportunity to serve an ad, our environment requires several pieces of information in order to produce a reward:

Ed: This is the latent education level of the user
Ad: The ad selected to be served to the user
Avail_ads: Which ads could have been served

The reward is either a click (1) or no click (0).

The reward function is a simple linear function which decreases the probability of returning a click the farther away the chosen ad is from the hidden education level.

Each education level is mapped to an integer

edu_map = {‘Preschool’: 1, ‘1st-4th’: 2, ‘5th-6th’: 3, ‘7th-8th’: 4, ‘9th’: 5, ‘10th’: 6, ‘11th’: 7, ‘12th’: 8, ‘HS-grad’: 9, ‘Some-college’: 10, ‘Assoc-acdm’: 11, ‘Assoc-voc’: 12, ‘Bachelors’: 13, ‘Prof-school’: 14, ‘Masters’: 15, ‘Doctorate’: 16}

and the distance between the hidden education level of the user and the chosen ad decreases the click probability from the base probability of a click that happens when the right ad is served:

prob = max(0, base_prob — delta * abs(edu_map[ed]- edu_map[ad])) + noise_scale

def display_ad(ed, ad, avail_ads, noise = True, base_prob = 0.2, delta = 0.025, noise_scale = 0.01):
    
    noise_scale = np.random.normal(scale = noise_scale) if noise else 0
    prob = max(0, base_prob - delta * abs(edu_map[ed]- ad)) + noise_scale
    
    uniform_draw = U()

    click = 1 if uniform_draw < prob else 0
    
    
    max_p = 0
    for ad_choice in avail_ads:
        p = max(0, base_prob - delta * abs(edu_map[ed]- edu_map[ad_choice]))

        if max_p < p:
            max_p =p
    
    best_click = 1 if uniform_draw < max_p else 0
    
    random_ad_indx = np.random.randint(0,len(avail_ads))
    
    random_prob = max(0, base_prob - delta * abs(edu_map[ed]- edu_map[avail_ads[random_ad_indx]])) + noise_scale
    random_click = 1 if uniform_draw < random_prob else 0
    
    return click, best_click, prob, max_p, random_prob, random_click

With a base probability of 0.2 (much too high for a real scenario), a penalty factor of 0.025 and a small amount of noise, the click probability for a user with (the hidden) education level of ‘HS-grad’ will change depending on the ad actually served. 500 simulations across each possible ad demonstrates this fall off that occurs as the ad is farther away from the optimal one which in this case is ‘HS-grad’ :

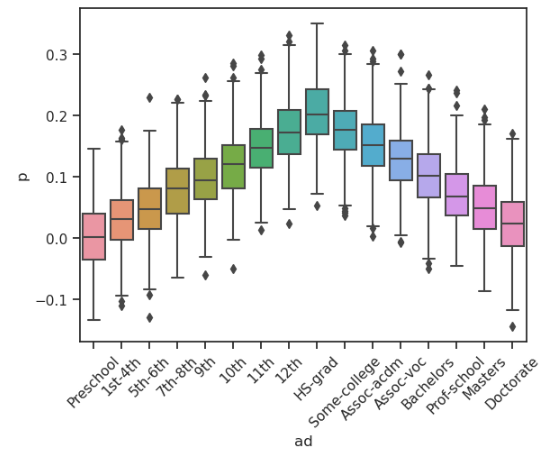
Once a click probability is generated, a click occurs or does not according to that probability. We also generate additional information from each opportunity:

• What is the optimal ad that could have been chosen from the available ones and what is that click probability (max_p)
• Did a click occur given this optimal ad choice (best_click)? This is a draw from a Bernoulli distribution with p equal to max_p.
• Pick a random ad from the available ones and what is that click probability (random_prob)
• Did a click occur given this random ad choice (random_click)? This is a draw from a Bernoulli distribution with p equal to random_prob.

Simulation

With these building blocks we can now construct a simulation from our environment. The steps follow

(repeat n times)….

1. Randomly sample a single user with replacement from the dataset. This includes their context and the latent education level

2. Randomly determine which of the ads are available for this context

3. Our policy determines which ad (action) to serve (take)

4. We log the click probability from our policy’s chosen ad, the best available ad choice and a random ad choice. We also log if a click occurred for each (chosen, best and random)

5. We update our policy with the tuple (context, action, reward)

This simple flow allows us to generate contexts, select an action and receive a reward. From this, we can see how bandit algorithms compare and how a given policy compares to a random policy and the best oracle.

Example

Now that we have outlined how our environment will work, what is missing is the definition of our policy which will learn to serve ads. There is a rich (and exhausting) literature on this topic from simple to sophisticated. Two really good sources to learn more is through several accessible papers and their respective implementations:

1. Contextual Bake Off and Vowpal Wabbit
2. Adapting MAB policies to Contextual bandit scenarios and repo

There are also ready made environment simulators such as Coba which is integrated with Vowpal Wabbit.

For this example we will use the simulation described above and for the policy, use a basic deep learning model with a binary output. The model has an embedding vector that is learned for each ad variant which is concatenated with the context vector for the user and then fed through several linear layers and a sigmoid.

class NN_CB(nn.Module):
 
 def __init__(self, num_ads, embed_dim, n_vars, hidden_size, drop_p):
 super(NN_CB, self).__init__()
 
 self.emb = nn.Embedding(num_embeddings = num_ads +1, embedding_dim = embed_dim, padding_idx = 0)
 
 self.linear1 = nn.Linear(embed_dim + n_vars, hidden_size)
 self.linear2 = nn.Linear(hidden_size, hidden_size//2)
 self.linear3 = nn.Linear(hidden_size//2, 1)
 self.relu = nn.ReLU()
 self.sigmoid = nn.Sigmoid()
 self.dropout = nn.Dropout(drop_p)
 
 def forward(self, a, x):
 emb = self.emb(a)

 x = torch.cat([torch.squeeze(emb, 1),x], dim = -1)
 
 x = self.linear1(x)
 x = self.relu(x)
 x = self.dropout(x)
 x = self.linear2(x)
 x = self.relu(x)
 x = self.dropout(x)
 x = self.linear3(x)
 x = self.sigmoid(x)
 
 return(x)

We created a function which is passed the current model, the context x and the available actions we could take (available ads). A hyperparameter epsilon is also included and if epsilon is smaller than the largest probability of a click returned by the model over the avaiulable ad choices, that ad is served. Otherwise, a random ad is served. This is a simple example of exploring versus exploiting.

def pick_action(mod, x, available_actions, epsilon):

    # The available ads for this opportunity as integers
    np_a = np.array([edu_map[ad] for ad in available_actions])

    # Repeat the context for each avaiable ad 
    x = x.repeat(len(available_actions)).reshape(len(available_actions),x.size()[0])
    a = torch.tensor(np_a).int().reshape(len(available_actions),1)

    # predict probability of a click from each available ad and then push through a softmax 
    mod.eval()
    p = mod(a,x)
    p = F.softmax(p,dim=0)

    
    # if the largest probability is higher than epsilon, select the max value as the chosen ad
    if torch.max(p) > epsilon:
        selected_indx = torch.argmax(p) 
        return(np_a[selected_indx])  # the integer value of the chosen ad
    
    # otherwise return a random index
    else:
        return(np.random.choice(np_a))

Epsilon is set for example at 0.25 initially. This would result in a random ad being served whenever the largest click probability from the model is less than 0.25. As the model becomes more confident in it’s prediction and times goes on — as epsilon is decayed as a function of time — the chance of a random ad becomes small. This is in essence just allowing some initial random serving of ads to build up a training dataset.

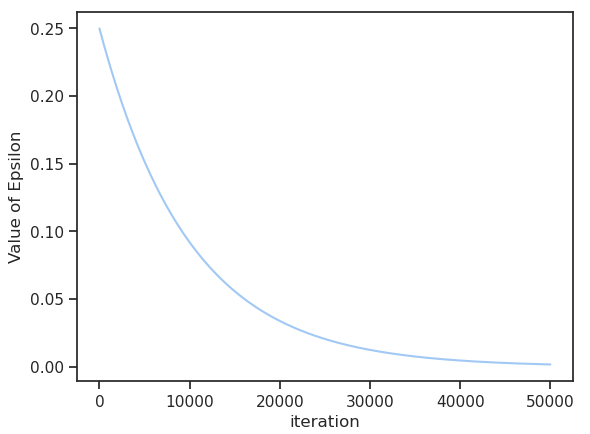
We set a few parameters and then run a loop (e.g. 100,000). As described above, we randomly sample an observation from the dataset and the available ads. We make a prediction, select the ad to serve, see if a click resulted and log the result. We also log the result of the best ad to have picked and a random ad. Every so often, we continue to train the model with the latest batch of context, the selected ad and the result.

N_ADS = 16
EMBED_DIM = 8
N_VARS = 78
HIDDEN_SIZE = 256
DROP_P = 0.2
LEARNING_RATE = 0.001
N_UPDATE_MOD = 64

epsilon = 0.25
decay = 0.9999


n_sim =100_000

hold_regret = []
hold_click = []
hold_random_click = []
hold_random_regret = []    


np_x = np.empty(shape=(0,N_VARS), dtype="float")
np_a = np.empty(shape=(0,1), dtype="int")
np_r = np.empty(shape=(0,1), dtype="int")


mod = NN_CB(num_ads = N_ADS, embed_dim = EMBED_DIM, n_vars = N_VARS, hidden_size = HIDDEN_SIZE, drop_p = DROP_P).double()
loss_fn = nn.BCELoss()
optimizer = torch.optim.Adam(mod.parameters(), lr = LEARNING_RATE) 


for i in range(n_sim):
    
    # generate a user (their hidden education level and the context of the opportunity)
    ed, context = generate_user(df_data)

    # what ads can we serve here?
    avail_ads = get_ad_inventory()

    # make preds and return best here
    x = torch.tensor(np.array(context)).double()
    
    ad_indx = pick_action(mod,x, avail_ads, epsilon)

        
        
    # append training data x and a
    np_x = np.append(np_x, np.array(context).reshape(1, N_VARS), axis=0)
    np_a = np.append(np_a, np.array([ad_indx]).reshape(1,1), axis=0)

    # did we get a click and would we if we had chosen the best option available?
    click, best_p_click, p, max_p, random_p, random_click = display_ad(ed, ad_indx, avail_ads, noise = True, base_prob=0.2)
    
    hold_regret.append(max_p - p)
    hold_random_regret.append(max_p - random_p)
    
    hold_click.append(click)
    hold_random_click.append(random_click) 
    
    np_r = np.append(np_r, np.array([click]).reshape(1,-1), axis=0)
    
    if i>0 and i %N_UPDATE_MOD == 0:
        # Train here
        mod,loss_fn, optimizer = update_mod(mod,loss_fn, optimizer, np_x, np_a, np_r)
            
            
        # Remove data from X and y
        np_x = np.empty(shape=(0,N_VARS), dtype="float")
        np_a = np.empty(shape=(0,1), dtype="int")
        np_r = np.empty(shape=(0,1), dtype="int")
    
    epsilon = epsilon * decay

At the end of 100,000 iterations (draw from the dataset) we plot the cumulative regret of the policy (our model) versus a random selection, which we could think of as what would have happened with equal sample sizes in an A/B test. Regret is how our policy faired against an oracle that always selected the best ad. We also plot the cumulative number of clicks.

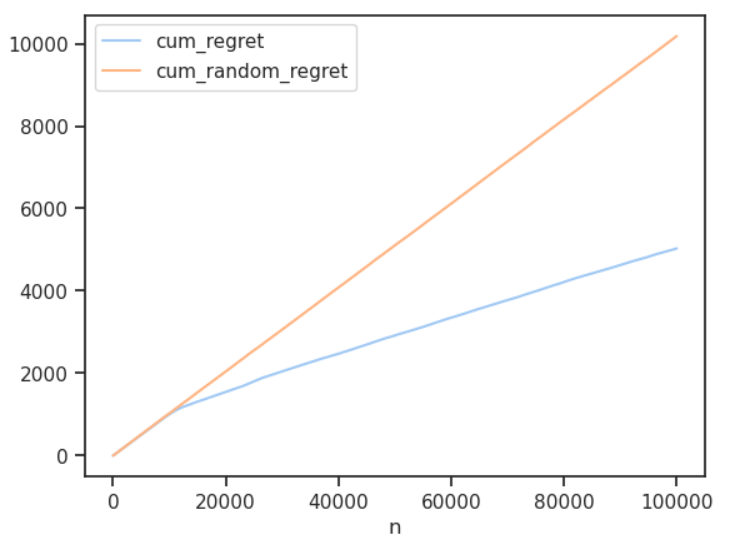
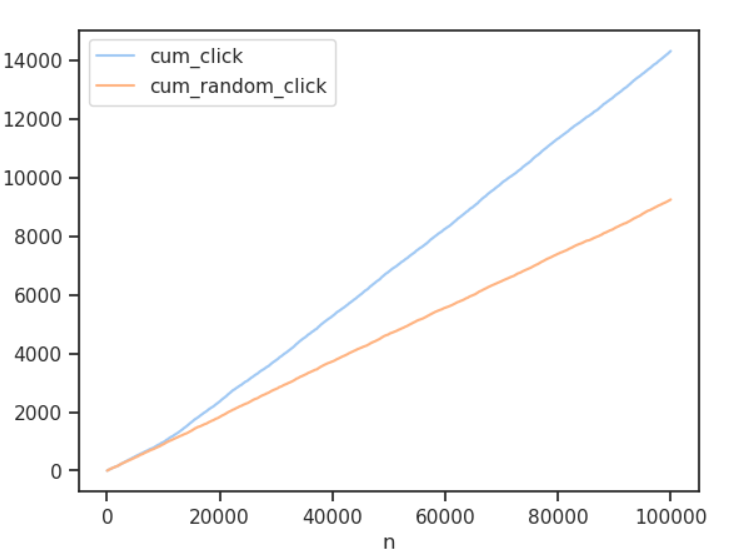
Through this simple simulation we have a means to compare the performance of various contextual bandits and tune our algorithm. Here we see how much more effective the model was than random serving.

Summary

Planned experimental designs (A/B tests) are vital for learning causal impacts of treatment decisions and necessary for effective marketing optimization. There are many cases where we are interested in rigorous statistical analysis of treatment effects and their contrasts, in order to determine valid confidence intervals around the effect size (overall or conditional on covariates).

There are other times when we are not able or willing to take that approach and we need to weigh the opportunity cost of running experiments — waiting and analyzing the results — versus optimizing within the campaign run without complete statistical grounding (i.e. power) and accepting the tradeoffs. Contextual bandits are one such option that work very well.

The topic of bandits in general is large and ever-evolving. Here we demonstrated a simple approach using a single ML model and saw convincing results which can be a springboard into the more specialized approaches to this type of optimization.

Credits:

1. All images by the author, unless otherwise noted.
2. The “Adult” Dataset credited to https://archive.ics.uci.edu/dataset/2/adult and used under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.

---

Contextual Bandit Simulation in Marketing was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

​When A/B Tests Are Not The Right ChoiceBandit Algorithm Or A/B Test?Imagine working as a Data Scientist for an adtech company and you are serving ads on behalf of a client. If that client comes to you and says that they have 2 variants in mind (i.e. changes to creative / message / offer ) for their upcoming campaign and they want to figure out “which ad is best”, what do you do? Run an A/B test where you randomly split the targeting units (people, devices, geographies) in half and serve one variant in each sample, let the campaign run and measure which ad produced the best result? Sounds reasonable!What if the client comes to you and says they have 25 ad variants in mind? Even at “adtech scale”, will there be enough measurable [clicks / visits / purchases] to support sufficient statistical power for the experiment?What if the client tells you that this campaign is not a recurring one where the knowledge gained for which ad is best, will be useful for the next campaign but instead that it is supporting a special event or one-off and wont be repeated (soon)? Does that change things?Standard statistical testing frameworks which we may position under the umbrella of A/B testing has its place and is rightfully popular in industry. There are cases where it completely breaks down though — as hinted at above. It can become infeasible to gather sufficient data during the course of an experiment to satisfy the demands of statistical power for rigorous experiments when there are more than a few treatments involved. Further, the premise of an A/B test is to devise treatment selection for future campaigns based on the results of past campaigns. If this isn’t an option — imagine a campaign for the launch of a new product or a seasonal event that wont be repeated for a year — while there may be some learning that can transfer, its unlikely that determining the exact best creative this time will be relevant next time. Plus, there is an opportunity cost involved with A/B tests. In order to measure all the variants involved, there will be a significant portion of the budget dedicated to low(er) performing ads over the duration of the campaign.In these situations, instead of an A/B test, a bandit algorithm can be utilized. In this case, we are less interested in high statistical confidence around the each treatment effect but we want to focus as much of the budget towards what we think seems like the best performing variant during the campaign.The basic idea of a bandit algorithm is that we learn a policy which maximizes the reward of the environment. In terms of our marketing example, this means we want to serve the ad variant which produces the highest KPI (e.g. click through rate) in the campaign (e.g. an online ad serving environment).Explaining bandit algorithms like multi-arm bandits is outside of the scope of this post, but at a high level, the key components are as follows:ArmsEach arm (e.g. ad variant) represents an option to choose.Each arm has an unknown reward distribution and the goal is to find the best arm over time.RewardsEach time an arm is pulled (e.g. ad served), it provides a reward (click or no click) from an unknown probability distribution.The objective is to maximize the total rewards.PolicyA policy is the strategy (i.e. model or rule) followed to decide which arm to pull at each opportunity.Exploration vs. Exploitation Trade-offExploration: Trying different arms to gather more information about their rewards.Exploitation: Selecting the arm that has provided the highest reward so far to maximize gains.The basic multi-arm bandit (MAB) algorithm (e.g. Thompson Sampling) seeks to find the best marginal arm. The goal in our scenario is to find the ad variant that produces the highest KPI for the entire population. Contextual Multi-arm bandits (CMAB) on the other hand, take this a step further and recognize that some arms may produce higher rewards with some segments of the population than others. Hence in marketing, we can personalize the ad being served.Environment SimulationIf the campaign is evergreen and we have no past results, we can simulate the outcomes and measure how well various algorithms work and debug our serving code. This is much easier in terms of an MAB than the contextual side. Now, if we happen to have access to logged data from a prior campaign where the arms were selected based on an existing policy, we can use that data to compare a new algorithm to an existing one.Another way we can explore the workings of a bandit algorithm and compare performance between optional implementations is through simulation, but instead of building this from scratch, we can instead repurpose any multiclass or multi-label dataset used for supervised learning.For this environment simulation, we will borrow heavily (with some changes) from an excellent example in Enes Bilgin’s Mastering Reinforcement Learning with Python. Lets walk through the situation and environment components piece by piece.DataThe environment will leverage an common dataset used for ML benchmarking and illustrates how a typical dataset used for classification and regression problems can be repurposed to be used by a CB application. The one chosen comes from the 1994 census and contains 32,561 rows and we will use 11 columns. A sample of the data follows, where we pay special attention to the Education column.There are 16 distinct levels of education ranging from “Preschool” to “Doctorate”Our first environmental function simply samples the dataset and returns a single observation. We then separate out the education value from the rest of the columns, which we call “context”.def generate_user(df_data): user = df_data.sample(1) # everything ed = user[‘education’] context = user.drop(‘education’, axis =1) context = context.values.tolist()[0] # all but education return ed.values.tolist()[0], contextSetupAt this point we need to explain the setup of the simulation. We are simulating an online advertising environment where users come to the application one at at time. In reality there is not an orderly queue of course but this doesn’t impact the generality of the simulation.We understand the context to contain information about the user, the specific state of the application, the time of day of the visit and other data. In our case the context is expressed through the 10 features in our dataset. These elements are all known and visible upon their arrival. The education level of the user is not known and is hidden from the policy. Our desire is to serve one of sixteen ads we have available, to the user in the hopes that they click on the ad.The education feature represents both a key aspect of the user and the available ads.Applicable AdsAt any point where we have an opportunity to serve an ad, not all ads are possible. We are adding this complexity to simulate a common occurrence where depending on the context (e.g. the web page or some user characteristic) not all available ads are appropriate.We accomplish this with a simple function where the available ads each have a fixed probability of being appropriate for the context. This is a simple uniform probability where each ad is randomly and independently included or excluded from the available inventory.def get_ad_inventory(prob = 0.8): ad_inventory = [] for level in available_ads: if U() < prob: # uniform prob U ad_inventory.append(level) # Make sure there are at least one ad if not ad_inventory: ad_inventory = get_ad_inventory() return ad_inventoryRewardFor each opportunity to serve an ad, our environment requires several pieces of information in order to produce a reward:Ed: This is the latent education level of the userAd: The ad selected to be served to the userAvail_ads: Which ads could have been servedThe reward is either a click (1) or no click (0).The reward function is a simple linear function which decreases the probability of returning a click the farther away the chosen ad is from the hidden education level.Each education level is mapped to an integeredu_map = {‘Preschool’: 1, ‘1st-4th’: 2, ‘5th-6th’: 3, ‘7th-8th’: 4, ‘9th’: 5, ‘10th’: 6, ‘11th’: 7, ‘12th’: 8, ‘HS-grad’: 9, ‘Some-college’: 10, ‘Assoc-acdm’: 11, ‘Assoc-voc’: 12, ‘Bachelors’: 13, ‘Prof-school’: 14, ‘Masters’: 15, ‘Doctorate’: 16}and the distance between the hidden education level of the user and the chosen ad decreases the click probability from the base probability of a click that happens when the right ad is served:prob = max(0, base_prob — delta * abs(edu_map[ed]- edu_map[ad])) + noise_scaledef display_ad(ed, ad, avail_ads, noise = True, base_prob = 0.2, delta = 0.025, noise_scale = 0.01): noise_scale = np.random.normal(scale = noise_scale) if noise else 0 prob = max(0, base_prob – delta * abs(edu_map[ed]- ad)) + noise_scale uniform_draw = U() click = 1 if uniform_draw < prob else 0 max_p = 0 for ad_choice in avail_ads: p = max(0, base_prob – delta * abs(edu_map[ed]- edu_map[ad_choice])) if max_p < p: max_p =p best_click = 1 if uniform_draw < max_p else 0 random_ad_indx = np.random.randint(0,len(avail_ads)) random_prob = max(0, base_prob – delta * abs(edu_map[ed]- edu_map[avail_ads[random_ad_indx]])) + noise_scale random_click = 1 if uniform_draw < random_prob else 0 return click, best_click, prob, max_p, random_prob, random_clickWith a base probability of 0.2 (much too high for a real scenario), a penalty factor of 0.025 and a small amount of noise, the click probability for a user with (the hidden) education level of ‘HS-grad’ will change depending on the ad actually served. 500 simulations across each possible ad demonstrates this fall off that occurs as the ad is farther away from the optimal one which in this case is ‘HS-grad’ :Click probability over 500 simulations when the user has HS-gradOnce a click probability is generated, a click occurs or does not according to that probability. We also generate additional information from each opportunity:What is the optimal ad that could have been chosen from the available ones and what is that click probability (max_p)Did a click occur given this optimal ad choice (best_click)? This is a draw from a Bernoulli distribution with p equal to max_p.Pick a random ad from the available ones and what is that click probability (random_prob)Did a click occur given this random ad choice (random_click)? This is a draw from a Bernoulli distribution with p equal to random_prob.SimulationWith these building blocks we can now construct a simulation from our environment. The steps follow(repeat n times)….1. Randomly sample a single user with replacement from the dataset. This includes their context and the latent education level2. Randomly determine which of the ads are available for this context3. Our policy determines which ad (action) to serve (take)4. We log the click probability from our policy’s chosen ad, the best available ad choice and a random ad choice. We also log if a click occurred for each (chosen, best and random)5. We update our policy with the tuple (context, action, reward)This simple flow allows us to generate contexts, select an action and receive a reward. From this, we can see how bandit algorithms compare and how a given policy compares to a random policy and the best oracle.ExampleNow that we have outlined how our environment will work, what is missing is the definition of our policy which will learn to serve ads. There is a rich (and exhausting) literature on this topic from simple to sophisticated. Two really good sources to learn more is through several accessible papers and their respective implementations:Contextual Bake Off and Vowpal WabbitAdapting MAB policies to Contextual bandit scenarios and repoThere are also ready made environment simulators such as Coba which is integrated with Vowpal Wabbit.For this example we will use the simulation described above and for the policy, use a basic deep learning model with a binary output. The model has an embedding vector that is learned for each ad variant which is concatenated with the context vector for the user and then fed through several linear layers and a sigmoid.class NN_CB(nn.Module): def __init__(self, num_ads, embed_dim, n_vars, hidden_size, drop_p): super(NN_CB, self).__init__() self.emb = nn.Embedding(num_embeddings = num_ads +1, embedding_dim = embed_dim, padding_idx = 0) self.linear1 = nn.Linear(embed_dim + n_vars, hidden_size) self.linear2 = nn.Linear(hidden_size, hidden_size//2) self.linear3 = nn.Linear(hidden_size//2, 1) self.relu = nn.ReLU() self.sigmoid = nn.Sigmoid() self.dropout = nn.Dropout(drop_p) def forward(self, a, x): emb = self.emb(a) x = torch.cat([torch.squeeze(emb, 1),x], dim = -1) x = self.linear1(x) x = self.relu(x) x = self.dropout(x) x = self.linear2(x) x = self.relu(x) x = self.dropout(x) x = self.linear3(x) x = self.sigmoid(x) return(x)We created a function which is passed the current model, the context x and the available actions we could take (available ads). A hyperparameter epsilon is also included and if epsilon is smaller than the largest probability of a click returned by the model over the avaiulable ad choices, that ad is served. Otherwise, a random ad is served. This is a simple example of exploring versus exploiting.def pick_action(mod, x, available_actions, epsilon): # The available ads for this opportunity as integers np_a = np.array([edu_map[ad] for ad in available_actions]) # Repeat the context for each avaiable ad x = x.repeat(len(available_actions)).reshape(len(available_actions),x.size()[0]) a = torch.tensor(np_a).int().reshape(len(available_actions),1) # predict probability of a click from each available ad and then push through a softmax mod.eval() p = mod(a,x) p = F.softmax(p,dim=0) # if the largest probability is higher than epsilon, select the max value as the chosen ad if torch.max(p) > epsilon: selected_indx = torch.argmax(p) return(np_a[selected_indx]) # the integer value of the chosen ad # otherwise return a random index else: return(np.random.choice(np_a))Epsilon is set for example at 0.25 initially. This would result in a random ad being served whenever the largest click probability from the model is less than 0.25. As the model becomes more confident in it’s prediction and times goes on — as epsilon is decayed as a function of time — the chance of a random ad becomes small. This is in essence just allowing some initial random serving of ads to build up a training dataset.We set a few parameters and then run a loop (e.g. 100,000). As described above, we randomly sample an observation from the dataset and the available ads. We make a prediction, select the ad to serve, see if a click resulted and log the result. We also log the result of the best ad to have picked and a random ad. Every so often, we continue to train the model with the latest batch of context, the selected ad and the result.N_ADS = 16EMBED_DIM = 8N_VARS = 78HIDDEN_SIZE = 256DROP_P = 0.2LEARNING_RATE = 0.001N_UPDATE_MOD = 64epsilon = 0.25decay = 0.9999n_sim =100_000hold_regret = []hold_click = []hold_random_click = []hold_random_regret = [] np_x = np.empty(shape=(0,N_VARS), dtype=”float”)np_a = np.empty(shape=(0,1), dtype=”int”)np_r = np.empty(shape=(0,1), dtype=”int”)mod = NN_CB(num_ads = N_ADS, embed_dim = EMBED_DIM, n_vars = N_VARS, hidden_size = HIDDEN_SIZE, drop_p = DROP_P).double()loss_fn = nn.BCELoss()optimizer = torch.optim.Adam(mod.parameters(), lr = LEARNING_RATE) for i in range(n_sim): # generate a user (their hidden education level and the context of the opportunity) ed, context = generate_user(df_data) # what ads can we serve here? avail_ads = get_ad_inventory() # make preds and return best here x = torch.tensor(np.array(context)).double() ad_indx = pick_action(mod,x, avail_ads, epsilon) # append training data x and a np_x = np.append(np_x, np.array(context).reshape(1, N_VARS), axis=0) np_a = np.append(np_a, np.array([ad_indx]).reshape(1,1), axis=0) # did we get a click and would we if we had chosen the best option available? click, best_p_click, p, max_p, random_p, random_click = display_ad(ed, ad_indx, avail_ads, noise = True, base_prob=0.2) hold_regret.append(max_p – p) hold_random_regret.append(max_p – random_p) hold_click.append(click) hold_random_click.append(random_click) np_r = np.append(np_r, np.array([click]).reshape(1,-1), axis=0) if i>0 and i %N_UPDATE_MOD == 0: # Train here mod,loss_fn, optimizer = update_mod(mod,loss_fn, optimizer, np_x, np_a, np_r) # Remove data from X and y np_x = np.empty(shape=(0,N_VARS), dtype=”float”) np_a = np.empty(shape=(0,1), dtype=”int”) np_r = np.empty(shape=(0,1), dtype=”int”) epsilon = epsilon * decayAt the end of 100,000 iterations (draw from the dataset) we plot the cumulative regret of the policy (our model) versus a random selection, which we could think of as what would have happened with equal sample sizes in an A/B test. Regret is how our policy faired against an oracle that always selected the best ad. We also plot the cumulative number of clicks.Cumulative regret over the 100,000 simulationsCumulative clicks over the 100,000 simulationsThrough this simple simulation we have a means to compare the performance of various contextual bandits and tune our algorithm. Here we see how much more effective the model was than random serving.SummaryPlanned experimental designs (A/B tests) are vital for learning causal impacts of treatment decisions and necessary for effective marketing optimization. There are many cases where we are interested in rigorous statistical analysis of treatment effects and their contrasts, in order to determine valid confidence intervals around the effect size (overall or conditional on covariates).There are other times when we are not able or willing to take that approach and we need to weigh the opportunity cost of running experiments — waiting and analyzing the results — versus optimizing within the campaign run without complete statistical grounding (i.e. power) and accepting the tradeoffs. Contextual bandits are one such option that work very well.The topic of bandits in general is large and ever-evolving. Here we demonstrated a simple approach using a single ML model and saw convincing results which can be a springboard into the more specialized approaches to this type of optimization.Credits:All images by the author, unless otherwise noted.The “Adult” Dataset credited to https://archive.ics.uci.edu/dataset/2/adult and used under a Creative Commons Attribution 4.0 International (CC BY 4.0) license.Contextual Bandit Simulation in Marketing was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.  multi-arm-bandit, data-science, marketing-analytics, targeting, contextual-marketing Towards Data Science – MediumRead More

Add to favorites