Ever wondered why the time to first token in LLMs is high but subsequent tokens are super fast?

In this post, I dive into the details of KV-Caching used in Mistral, a topic I initially found quite daunting. However, as I delved deeper, it became a fascinating subject, especially when it explained why the time to first token (TTFT) in these language models is generally high — a pattern I noticed during countless API calls 🙂.

I’ll cover:

1. What exactly is KV-Caching?
2. The concept of the rolling cache buffer
3. The prefill and decode stages
4. Formulating attention masks with the help of the xFormers library

KV-Caching: Avoiding Redundant Computations

Imagine our input token sequence as x1, x2, x3 … xt, and we’re determining the output at time step t. To find the attention output (at each transformer layer), we need the dot product of the current token’s query vector with the key vectors of the current and preceding tokens. After normalizing via softmax, these become the attention weights over the value vectors. Here are two key observations:

1. Single Token Decoding: Decoding happens one token at a time. We’re only interested in the self-attention output for the current token, focusing solely on its query vector, not query vectors of other tokens.
2. Precomputed Keys and Values: We need the dot product with the keys of preceding tokens, which were already computed when calculating the self-attention output of the token at time step t−1. The same goes for the value vectors.

The dimensions of the key quantities are as follows:

1. Token Embedding Vectors: dim
2. Dimension of Query, Key, Value Heads: head_dim
3. Number of Query Heads: n_heads
4. Number of Key and Value Heads: n_kv_heads
5. Number of Transformer Layers: n_layers

(Note: Mistral uses grouped query attention where for each token, 4 of its query vectors attend to the same key-value pair. With n_heads=32, we have n_kv_heads=32/4=8)

In the unoptimized implementation:

Assuming a single transformer layer, at each time step, we calculate the query for the current token, and the key and value vectors for both the current and preceding tokens. This process involves three matrix multiplications.

a. Query Calculation (Q):

b. Key Calculation (K):

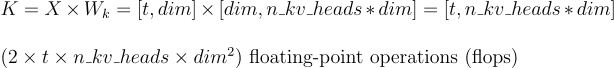
c. Value Calculation (V):

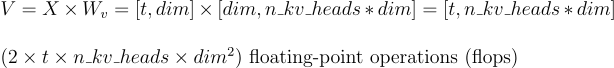
Once we have the query, key and value vectors we can then proceed to compute the attention output using —

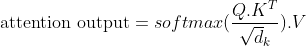
In the optimized implementation:

However, as mentioned in point 2, the keys and values of tokens up to time step t−1 would have already been computed when determining the output at time step t−1. This means we can avoid redundant computations by storing the keys and values of tokens up to time step t−1.

Note: Mistral uses a sliding window attention mechanism, so we only attend to a specific number of previous tokens. More details on this will be covered later.

What this means is that during decoding, we compute the key and value vectors only for the current token and not for the previous ones. So, operations (b) and (c) above are performed for just one token instead of t tokens. Specifically:

Key Calculation (K):

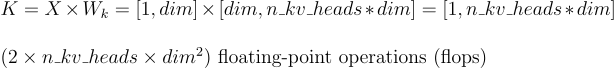
Value Calculation (V):

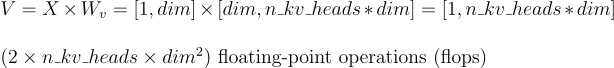
FLOPS Saved

At every step of decoding, we save 2*(t-1)*n_kv_heads*dim² FLOPS. For a sequence of length T, this translates to savings of 2*(T*(T-1)/2)*n_kv_heads*dim²FLOPS.

Considering we’ve assumed a single transformer layer, and knowing that Mistral utilizes 32 transformer layers, the savings are multiplied by 32. This is significant!

For a typical sequence length of 10,000 tokens, with n_kv_heads=8 and dim=4096, we get 4.294e+17 FLOPS (10000*10000*8*4096*4096*32)

An Nvidia A100 GPU has approximately 312e+12 FLOPS, meaning we would save around 23 minutes in generating this sequence of 10,000 tokens!

Note: This is a simplified calculation to give an idea of the benefits, which are indeed substantial. Actual improvements will depend on various factors such as maximum feasible cache size, GPU memory, parallelization with multiple GPUs, etc.

Now that we understand the KV cache, I’ll discuss how we leverage it during output generation!

Prefill and Decode Stages

First, let’s establish some terminology used by Mistral:

1. Sliding Window Attention (SWA): Mistral uses SWA, meaning each token attends to itself and the previous W−1 tokens, where W is the window size.
2. KV Cache Size: We set our KV Cache to size W. This means we can store W key vectors and W value vectors in the cache. This ensures we have the necessary context to compute the self-attention output for the next token.
3. Chunk Size: We process user input prompt sequences also W tokens at a time (more on this in the next section on Prefill). This chunk size limits GPU memory usage. Self-attention requires K, Q, and V to be on the GPU, and these grow with the input size, making it impractical to process the entire input sequence in one batch.

Note:

Each transformer layer in Mistral has its own separate KV Cache.

At first, it might seem (it did to me!) that calculating and caching only the keys and values of the last W-1 tokens in the input sequence would be sufficient to generate the first output token. However, that’s not the case! This is because Mistral has more than one transformer layer. To compute the output from the second layer of our next token, we need the output of the last W−1 tokens in the first layer, which in turn depends on the last (2W−1) input tokens (similar to receptive field in CNNs!)

Mistral uses a window size of W = 4096 tokens.

Part 1: Prefill Stage

The input to these models usually starts with user-provided tokens (the well-known user prompt 😊), followed by the generation of output tokens. The stage where we populate the KV-cache with the keys and values from the user prompt, so we can use them when generating output tokens, is called the prefill stage. This is the key reason why the time to first token (TTFT) is generally high.

To understand the workings of the prefill stage, let’s walk through an example:

Imagine we have 3 sequences in our inference batch with user prompt token lengths of 4, 1, and 3 respectively. Suppose we have a window size W=3, and we want to generate the next 5 tokens for each sequence.

Given:

1. seqlens = [4,1,3]
2. sliding_window_size = cache_size = 3
3. chunk_size = 2 (for illustration purposes, ideally this would also be = W = 3 as mentioned before)

In the prefill stage, since we already have all the input tokens, we can process them in parallel. With a chunk_size of 2 we require two iterations as explained below.

Iteration 1

We have a chunk size of 2, so we’ll process the first 2 tokens from each sequence. This means the sequence lengths under consideration for this step are [2,1,2].

To batch the 3 sequences, one approach is to pad the shorter sequences to match the longest sequence. However, if the sequences vary greatly in length, padding results in a lot of wasted memory. Hence, this approach is generally not used.

The preferred approach is to concatenate all the sequences in the batch into a single larger sequence. We will create an appropriate attention mask so that tokens attend only to those within the same sequence.

This implies our input shape is: [2+1+2,dim] = [5,dim]

We compute our Q, K, and V vectors for this input by multiplying with matrices Wq, Wk, and Wv. Assuming the number of heads = 1 for simplicity, the outputs will have the following shapes:

a. Q: [5, head_dim]

b. K: [5, head_dim]

c. V: [5, head_dim]

Next, we add rotary positional encodings to our Q and K vectors.

With these preparations, we are ready to calculate the self-attention output!

Step 1: Retrieve from KV-Cache and Compute Attention

Since this is the first chunk, we look at the KV-cache and find it empty — no vectors stored there. This means there are no previous tokens to attend to, only the current token itself. Consequently, the number of key-value vectors (kv_seqlen) matches the number of query vectors (q_seqlen) in each sequence.

To handle this, we create our mask using the BlockDiagonalCausalMask from the xFormers library like so:

mask = BlockDiagonalCausalMask.from_seqlens(q_seqlen = [2,1,2], kv_seqlen=[2,1,2]).make_local_attention(window_size=3)

The attention mask can be visualized using

mask.materialize(shape=(5,5)).exp()
# The 'shape' argument is obtained as follows: the first dimension is the total number of query vectors and the second dimension is the total number of key/value vectors

and the output is

[[1., 0., 0., 0., 0.],
 [1., 1., 0., 0., 0.],
 [0., 0., 1., 0., 0.],
 [0., 0., 0., 1., 0.],
 [0., 0., 0., 1., 1.]]

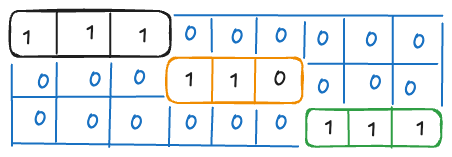
Let’s understand how we obtained this mask and why it makes sense. Focus on q_seqlen = [2,1,2] and kv_seqlen=[2,1,2].

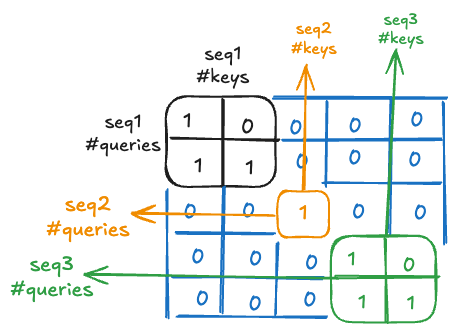
The first sequence has 2 query vectors and 2 key-value (kv) vectors. The attention mask for this sequence is the 2×2 matrix in the top left:

[[1,0],
[1,1]]

The second element in the first row is 0 because this is a causal mask, and we do not want the first token to attend to the second token (in the future).

The second sequence has just 1 query and 1 kv vector, represented by the center 1×1 matrix. The third sequence, similar to the first, has an identical 2×2 matrix in the bottom right.

Notice that the attention masks for the sequences are logically concatenated along the diagonal.

Setting the window size to 3 in our mask creation ensures that we only consider up to 3 tokens for attention per sequence.

This mask is applied to the output of the matrix product of Q and K.T. Thus, dot products of queries and keys from different sequences are nullified by the 0s in the combined attention matrix, preserving causality.

Note: Under the hood, xFormers does not calculate those dot products at all that would be nullified by the 0s by the attention mask

The BlockDiagonalCausalMask in xFormers starts filling 1s from the top-left of each block, which is exactly what we need for our first prefill.

Step 2: Cache Update

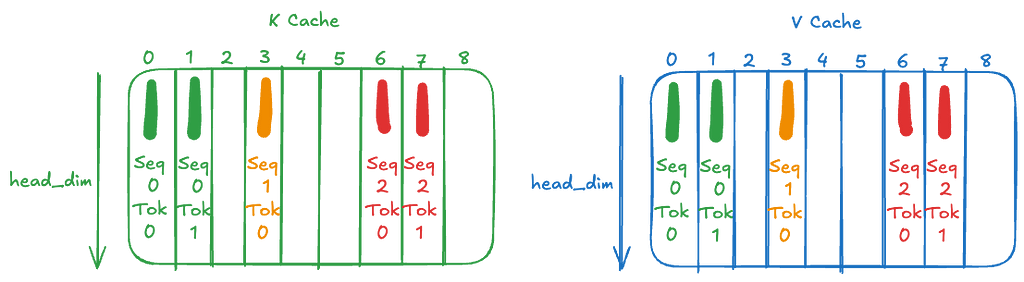
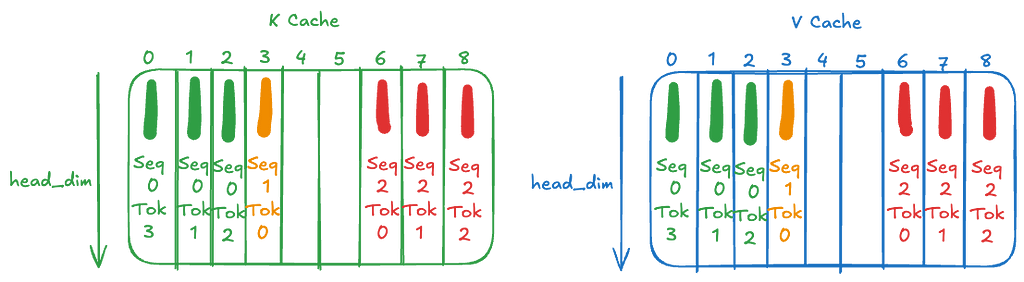
Next, we update the cache with the computed keys and values. Our cache size is initialized to W×batch_size=W×3 that is one for each sequence and one each for key and values. This is a rolling cache meaning tokens in the first sequence will use up cache positions [0, 1, 2, 0, 1, 2 …], tokens in the second sequence will use up cache positions [3, 4, 5, 3, 4, 5 …] and tokens in the third sequence will use up cache positions [6, 7, 8, 6, 7, 8 …].

So, our KV-Cache after the first iteration (on processing 2, 1 and 2 number of tokens from each sequence) looks like this:

Iteration 2

We now move on to the remaining part of our sequences. The remaining tokens to process for each sequence are [2, 0, 1]. In Mistral code, this stage is referred to as the ‘subsequent prefill’ stage.

Step 1: Retrieve from KV-Cache and Compute Attention

As in iteration 1, we first look at the KV-cache but now we find entries in them. We retrieve the entries and perform and an unroll/unrotate step on them to restore the correct sequence order. Why do we do this?

Remember, this is a rolling cache. If we had processed, say, 5 tokens, the queries and values for the 4th and 5th tokens would occupy the first two cache positions, followed by those of the 3rd token. After unrolling, we would have the queries and values of the 3rd, 4th, and 5th tokens in that order. However, in this case, since we haven’t processed more than 3 tokens, the current cache order matches the token order.

Note: The reason we need to unrotate is that during the prefill stage, we process multiple tokens per sequence and we need to identify which queries should attend to which keys in the sequence. In contrast, during the decode stage (described in the following section), we process only one token of a sequence at a time. In that case, unrotation isn’t necessary because this single token will attend to all elements in the cache.

Currently, the number of query vectors for each sequence is [2, 0, 1]. The number of key vectors is calculated as the number of query vectors plus the number of valid entries in the cache:

kv_seqlen = [2+2, 0+1, 1+2] = [4, 1, 3]

We create the mask using the make_local_attention_from_bottomright() method of the BlockDiagonalMask class from xFormers:

BlockDiagonalMask.from_seqlens(
  q_seqlen=[2,0,1],
  kv_seqlen=[4,1,3],
).make_local_attention_from_bottomright(window_size=3)

This mask looks like:

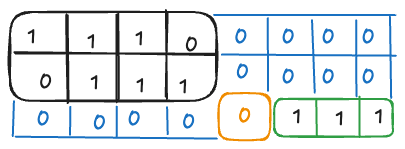
Similar to the logic explained in Iteration 1, we have three matrices concatenated diagonally, where the rows represent the number of queries and the columns represent the number of keys in each sequence.

Here, we need to use make_local_attention_from_bottomright() instead of make_local_attention(), as we want to start from the bottom right in each block.

Step 2: Cache Update

We store the computed keys and values into the cache similar to iteration 1 in a rolling fashion. Our updated cache then looks like this:

Part 2: Decode Stage

After the prefill stage, we move on to the decode stage, where we begin generating our output tokens one at a time.

Unlike the prefill stage, where Step 1 involves reading cache entries and computing attention and Step 2 involves updating the cache with the new entries, in the decode stage we reverse these steps. First, we update the cache with the new entries, and then we read all the entries (including the ones we just added) to compute self-attention.

This approach works neatly because decoding happens one token at a time, and we know all entries in the cache are within our context window (of size W) and needed for self-attention.

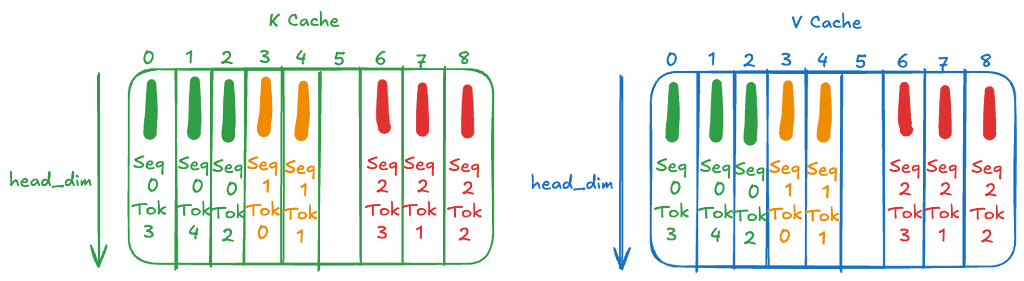
Step 1: Cache Update

We compute the key and value vectors for the current input token and add them to the cache. The new tokens are #4, #1 and #3 for the three sequences. The updated cache looks like this:

Step 2: Retrieve from KV-Cache and Compute Attention

We now proceed to compute self-attention and the associated mask!

1. We have one query for each sequence in the batch, so
   q_seqlen= [1, 1, 1].
2. The number of keys is the number of valid entries in the cache, given by kv_seqlen = [3, 2, 3].

In the Mistral codebase, for simplicity, they fix the attention mask shape to (W×batch_size, W×batch_size) = (9,9)

We create our attention mask again with xFormers like so:

BlockDiagonalCausalWithOffsetPaddedKeysMask.from_seqlens(
  q_seqlen=[1,1,1],
  kv_padding=3,
  kv_seqlen=[3,2,3]
)

This mask looks like:

We have 3 blocks of 1×3 matrices concatenated diagonally. Since we fixed our attention mask to 9×9 for simplicity, our initial attention score matrix (before applying the mask) considers dot products between all queries in the cache (valid or not) with all keys. This is evident, for example, in sequence 2 above, where we place a 0 in the 3rd entry of the block to invalidate that entry.

And that’s a wrap! I hope you found this post both enjoyable and enlightening. Thanks for reading, and I look forward to sharing more of my learnings!

References

1. Mistral Codebase: https://github.com/mistralai/mistral-inference/tree/main
2. xFormers Codebase: https://github.com/facebookresearch/xformers
3. Umar Jamil’s excellent overview of Mistral: https://www.youtube.com/watch?v=UiX8K-xBUpE

---

Deep Dive into KV-Caching In Mistral was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

​Ever wondered why the time to first token in LLMs is high but subsequent tokens are super fast?In this post, I dive into the details of KV-Caching used in Mistral, a topic I initially found quite daunting. However, as I delved deeper, it became a fascinating subject, especially when it explained why the time to first token (TTFT) in these language models is generally high — a pattern I noticed during countless API calls 🙂.I’ll cover:What exactly is KV-Caching?The concept of the rolling cache bufferThe prefill and decode stagesFormulating attention masks with the help of the xFormers libraryKV-Caching: Avoiding Redundant ComputationsImagine our input token sequence as x1, x2, x3 … xt, and we’re determining the output at time step t. To find the attention output (at each transformer layer), we need the dot product of the current token’s query vector with the key vectors of the current and preceding tokens. After normalizing via softmax, these become the attention weights over the value vectors. Here are two key observations:Single Token Decoding: Decoding happens one token at a time. We’re only interested in the self-attention output for the current token, focusing solely on its query vector, not query vectors of other tokens.Precomputed Keys and Values: We need the dot product with the keys of preceding tokens, which were already computed when calculating the self-attention output of the token at time step t−1. The same goes for the value vectors.The dimensions of the key quantities are as follows:Token Embedding Vectors: dimDimension of Query, Key, Value Heads: head_dimNumber of Query Heads: n_headsNumber of Key and Value Heads: n_kv_headsNumber of Transformer Layers: n_layers(Note: Mistral uses grouped query attention where for each token, 4 of its query vectors attend to the same key-value pair. With n_heads=32, we have n_kv_heads=32/4=8)In the unoptimized implementation:Assuming a single transformer layer, at each time step, we calculate the query for the current token, and the key and value vectors for both the current and preceding tokens. This process involves three matrix multiplications.a. Query Calculation (Q):b. Key Calculation (K):c. Value Calculation (V):Once we have the query, key and value vectors we can then proceed to compute the attention output using —In the optimized implementation:However, as mentioned in point 2, the keys and values of tokens up to time step t−1 would have already been computed when determining the output at time step t−1. This means we can avoid redundant computations by storing the keys and values of tokens up to time step t−1.Note: Mistral uses a sliding window attention mechanism, so we only attend to a specific number of previous tokens. More details on this will be covered later.What this means is that during decoding, we compute the key and value vectors only for the current token and not for the previous ones. So, operations (b) and (c) above are performed for just one token instead of t tokens. Specifically:Key Calculation (K):Value Calculation (V):FLOPS SavedAt every step of decoding, we save 2*(t-1)*n_kv_heads*dim² FLOPS. For a sequence of length T, this translates to savings of 2*(T*(T-1)/2)*n_kv_heads*dim²FLOPS.Considering we’ve assumed a single transformer layer, and knowing that Mistral utilizes 32 transformer layers, the savings are multiplied by 32. This is significant!For a typical sequence length of 10,000 tokens, with n_kv_heads=8 and dim=4096, we get 4.294e+17 FLOPS (10000*10000*8*4096*4096*32)An Nvidia A100 GPU has approximately 312e+12 FLOPS, meaning we would save around 23 minutes in generating this sequence of 10,000 tokens!Note: This is a simplified calculation to give an idea of the benefits, which are indeed substantial. Actual improvements will depend on various factors such as maximum feasible cache size, GPU memory, parallelization with multiple GPUs, etc.Now that we understand the KV cache, I’ll discuss how we leverage it during output generation!Prefill and Decode StagesFirst, let’s establish some terminology used by Mistral:Sliding Window Attention (SWA): Mistral uses SWA, meaning each token attends to itself and the previous W−1 tokens, where W is the window size.KV Cache Size: We set our KV Cache to size W. This means we can store W key vectors and W value vectors in the cache. This ensures we have the necessary context to compute the self-attention output for the next token.Chunk Size: We process user input prompt sequences also W tokens at a time (more on this in the next section on Prefill). This chunk size limits GPU memory usage. Self-attention requires K, Q, and V to be on the GPU, and these grow with the input size, making it impractical to process the entire input sequence in one batch.Note:Each transformer layer in Mistral has its own separate KV Cache.At first, it might seem (it did to me!) that calculating and caching only the keys and values of the last W-1 tokens in the input sequence would be sufficient to generate the first output token. However, that’s not the case! This is because Mistral has more than one transformer layer. To compute the output from the second layer of our next token, we need the output of the last W−1 tokens in the first layer, which in turn depends on the last (2W−1) input tokens (similar to receptive field in CNNs!)Mistral uses a window size of W = 4096 tokens.Part 1: Prefill StageThe input to these models usually starts with user-provided tokens (the well-known user prompt 😊), followed by the generation of output tokens. The stage where we populate the KV-cache with the keys and values from the user prompt, so we can use them when generating output tokens, is called the prefill stage. This is the key reason why the time to first token (TTFT) is generally high.To understand the workings of the prefill stage, let’s walk through an example:Imagine we have 3 sequences in our inference batch with user prompt token lengths of 4, 1, and 3 respectively. Suppose we have a window size W=3, and we want to generate the next 5 tokens for each sequence.Given:seqlens = [4,1,3]sliding_window_size = cache_size = 3chunk_size = 2 (for illustration purposes, ideally this would also be = W = 3 as mentioned before)In the prefill stage, since we already have all the input tokens, we can process them in parallel. With a chunk_size of 2 we require two iterations as explained below.Iteration 1We have a chunk size of 2, so we’ll process the first 2 tokens from each sequence. This means the sequence lengths under consideration for this step are [2,1,2].To batch the 3 sequences, one approach is to pad the shorter sequences to match the longest sequence. However, if the sequences vary greatly in length, padding results in a lot of wasted memory. Hence, this approach is generally not used.The preferred approach is to concatenate all the sequences in the batch into a single larger sequence. We will create an appropriate attention mask so that tokens attend only to those within the same sequence.This implies our input shape is: [2+1+2,dim] = [5,dim]We compute our Q, K, and V vectors for this input by multiplying with matrices Wq, Wk, and Wv. Assuming the number of heads = 1 for simplicity, the outputs will have the following shapes:a. Q: [5, head_dim]b. K: [5, head_dim]c. V: [5, head_dim]Next, we add rotary positional encodings to our Q and K vectors.With these preparations, we are ready to calculate the self-attention output!Step 1: Retrieve from KV-Cache and Compute AttentionSince this is the first chunk, we look at the KV-cache and find it empty — no vectors stored there. This means there are no previous tokens to attend to, only the current token itself. Consequently, the number of key-value vectors (kv_seqlen) matches the number of query vectors (q_seqlen) in each sequence.To handle this, we create our mask using the BlockDiagonalCausalMask from the xFormers library like so:mask = BlockDiagonalCausalMask.from_seqlens(q_seqlen = [2,1,2], kv_seqlen=[2,1,2]).make_local_attention(window_size=3)The attention mask can be visualized usingmask.materialize(shape=(5,5)).exp()# The ‘shape’ argument is obtained as follows: the first dimension is the total number of query vectors and the second dimension is the total number of key/value vectorsand the output is[[1., 0., 0., 0., 0.], [1., 1., 0., 0., 0.], [0., 0., 1., 0., 0.], [0., 0., 0., 1., 0.], [0., 0., 0., 1., 1.]]Let’s understand how we obtained this mask and why it makes sense. Focus on q_seqlen = [2,1,2] and kv_seqlen=[2,1,2].Image by authorThe first sequence has 2 query vectors and 2 key-value (kv) vectors. The attention mask for this sequence is the 2×2 matrix in the top left:[[1,0],[1,1]]The second element in the first row is 0 because this is a causal mask, and we do not want the first token to attend to the second token (in the future).The second sequence has just 1 query and 1 kv vector, represented by the center 1×1 matrix. The third sequence, similar to the first, has an identical 2×2 matrix in the bottom right.Notice that the attention masks for the sequences are logically concatenated along the diagonal.Setting the window size to 3 in our mask creation ensures that we only consider up to 3 tokens for attention per sequence.This mask is applied to the output of the matrix product of Q and K.T. Thus, dot products of queries and keys from different sequences are nullified by the 0s in the combined attention matrix, preserving causality.Note: Under the hood, xFormers does not calculate those dot products at all that would be nullified by the 0s by the attention maskThe BlockDiagonalCausalMask in xFormers starts filling 1s from the top-left of each block, which is exactly what we need for our first prefill.Step 2: Cache UpdateNext, we update the cache with the computed keys and values. Our cache size is initialized to W×batch_size=W×3 that is one for each sequence and one each for key and values. This is a rolling cache meaning tokens in the first sequence will use up cache positions [0, 1, 2, 0, 1, 2 …], tokens in the second sequence will use up cache positions [3, 4, 5, 3, 4, 5 …] and tokens in the third sequence will use up cache positions [6, 7, 8, 6, 7, 8 …].So, our KV-Cache after the first iteration (on processing 2, 1 and 2 number of tokens from each sequence) looks like this:Image by authorIteration 2We now move on to the remaining part of our sequences. The remaining tokens to process for each sequence are [2, 0, 1]. In Mistral code, this stage is referred to as the ‘subsequent prefill’ stage.Step 1: Retrieve from KV-Cache and Compute AttentionAs in iteration 1, we first look at the KV-cache but now we find entries in them. We retrieve the entries and perform and an unroll/unrotate step on them to restore the correct sequence order. Why do we do this?Remember, this is a rolling cache. If we had processed, say, 5 tokens, the queries and values for the 4th and 5th tokens would occupy the first two cache positions, followed by those of the 3rd token. After unrolling, we would have the queries and values of the 3rd, 4th, and 5th tokens in that order. However, in this case, since we haven’t processed more than 3 tokens, the current cache order matches the token order.Note: The reason we need to unrotate is that during the prefill stage, we process multiple tokens per sequence and we need to identify which queries should attend to which keys in the sequence. In contrast, during the decode stage (described in the following section), we process only one token of a sequence at a time. In that case, unrotation isn’t necessary because this single token will attend to all elements in the cache.Currently, the number of query vectors for each sequence is [2, 0, 1]. The number of key vectors is calculated as the number of query vectors plus the number of valid entries in the cache:kv_seqlen = [2+2, 0+1, 1+2] = [4, 1, 3]We create the mask using the make_local_attention_from_bottomright() method of the BlockDiagonalMask class from xFormers:BlockDiagonalMask.from_seqlens( q_seqlen=[2,0,1], kv_seqlen=[4,1,3],).make_local_attention_from_bottomright(window_size=3)This mask looks like:Image by authorSimilar to the logic explained in Iteration 1, we have three matrices concatenated diagonally, where the rows represent the number of queries and the columns represent the number of keys in each sequence.Here, we need to use make_local_attention_from_bottomright() instead of make_local_attention(), as we want to start from the bottom right in each block.Step 2: Cache UpdateWe store the computed keys and values into the cache similar to iteration 1 in a rolling fashion. Our updated cache then looks like this:Image by authorPart 2: Decode StageAfter the prefill stage, we move on to the decode stage, where we begin generating our output tokens one at a time.Unlike the prefill stage, where Step 1 involves reading cache entries and computing attention and Step 2 involves updating the cache with the new entries, in the decode stage we reverse these steps. First, we update the cache with the new entries, and then we read all the entries (including the ones we just added) to compute self-attention.This approach works neatly because decoding happens one token at a time, and we know all entries in the cache are within our context window (of size W) and needed for self-attention.Step 1: Cache UpdateWe compute the key and value vectors for the current input token and add them to the cache. The new tokens are #4, #1 and #3 for the three sequences. The updated cache looks like this:Image by authorStep 2: Retrieve from KV-Cache and Compute AttentionWe now proceed to compute self-attention and the associated mask!We have one query for each sequence in the batch, so q_seqlen= [1, 1, 1].The number of keys is the number of valid entries in the cache, given by kv_seqlen = [3, 2, 3].In the Mistral codebase, for simplicity, they fix the attention mask shape to (W×batch_size, W×batch_size) = (9,9)We create our attention mask again with xFormers like so:BlockDiagonalCausalWithOffsetPaddedKeysMask.from_seqlens( q_seqlen=[1,1,1], kv_padding=3, kv_seqlen=[3,2,3])This mask looks like:Image by authorWe have 3 blocks of 1×3 matrices concatenated diagonally. Since we fixed our attention mask to 9×9 for simplicity, our initial attention score matrix (before applying the mask) considers dot products between all queries in the cache (valid or not) with all keys. This is evident, for example, in sequence 2 above, where we place a 0 in the 3rd entry of the block to invalidate that entry.And that’s a wrap! I hope you found this post both enjoyable and enlightening. Thanks for reading, and I look forward to sharing more of my learnings!ReferencesMistral Codebase: https://github.com/mistralai/mistral-inference/tree/mainxFormers Codebase: https://github.com/facebookresearch/xformersUmar Jamil’s excellent overview of Mistral: https://www.youtube.com/watch?v=UiX8K-xBUpEDeep Dive into KV-Caching In Mistral was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.  kv-cache, genai, mistral, large-language-models, transformers Towards Data Science – MediumRead More

Add to favorites