How can numerical user metrics, such as “3 visits in the past week,” be transformed into a personalized assessment of whether this behavior is typical or unusual for the user?

In almost any digital product, analysts often face the challenge of building a digital customer profile — a set of parameters that describe the customer’s state and behavior in one way or another.

What are the potential applications of these metrics?

• Gaining insights into user behavior
• Leveraging as features in ML models
• Developing business rules for personalized offers

A simple example is e-commerce, with metrics like those listed in the table below.

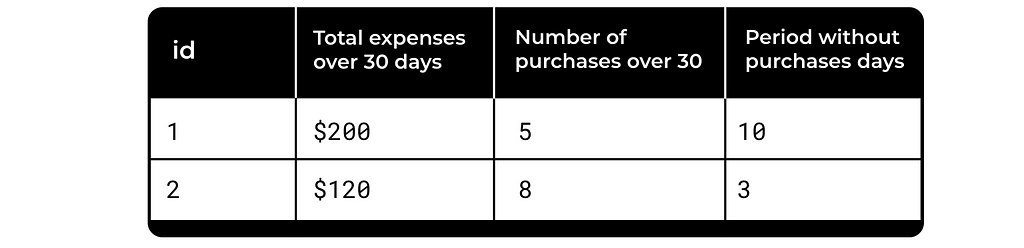
These metrics are used everywhere, but what is the problem with them? They don’t take into account the specific user’s history or the dynamics of this particular metric. Is $200 spend a lot for user 1? It’s unclear. Yet this distinction significantly influences the business decision we make next.

Even within the context of a single user, $200 can have a different meaning for the business depending on the user’s stage in their lifecycle with the product. $200 spent during the user onboarding, pick activity and re-activation are different.

We’d like to have some normalized metrics to be able compare them between users. Something like this:

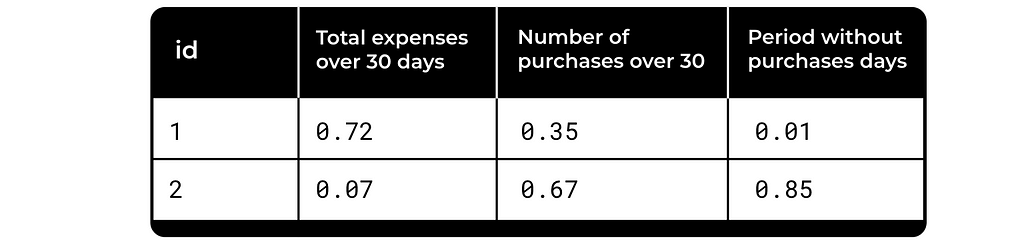
So how can we move from a numerical description of customer behavior to a more characteristic representation? For instance, how can the fact that “a customer hasn’t made a transaction for 7 days” be translated into an individualized assessment of whether this is unusual or typical for that specific customer? The challenge is to achieve this without losing interpretability, preserving business relevance, and avoiding black-box models.

A simple approach is to analyze the distribution of the metric and determine the probability of observing the current result (i.e., calculate the p-value). This helps us understand how extreme the value is compared to the user’s history.

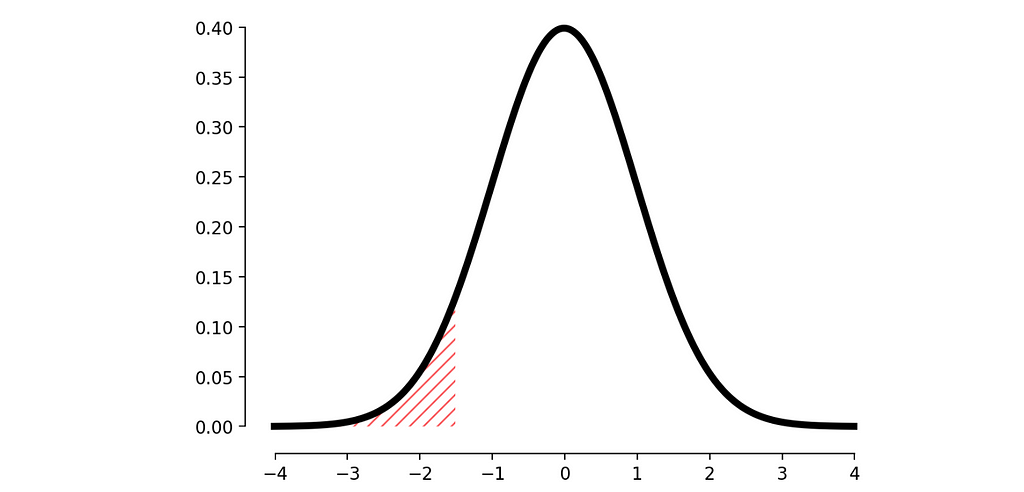
But what’s the challenge here? In most cases, the distribution of metrics is not normal, making p-value calculations more complex.

The random metric probably would have a distribution similar to this one:

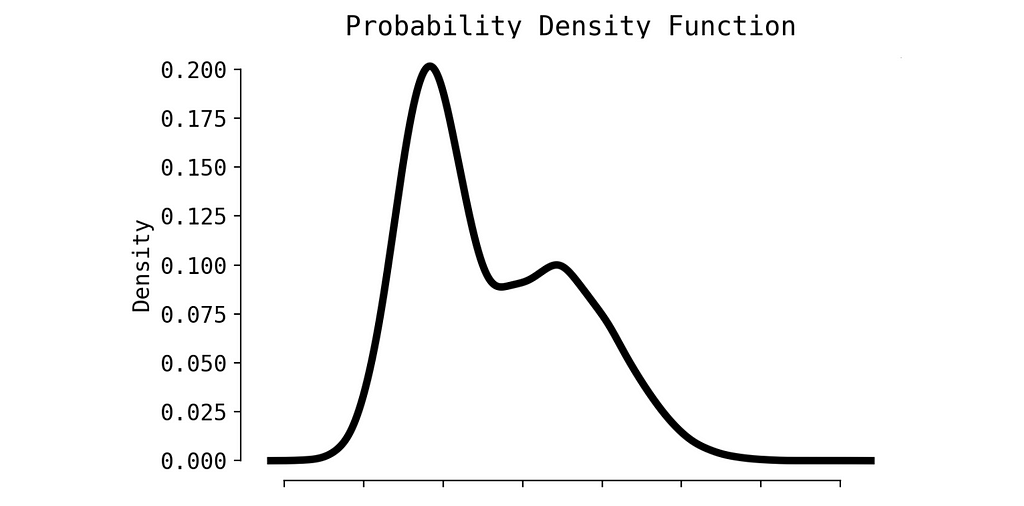
We can apply some small trick and to transform Probability Density Function to Cumulative Distribution Function (CDF). Calculating p-value in this case is much easier.

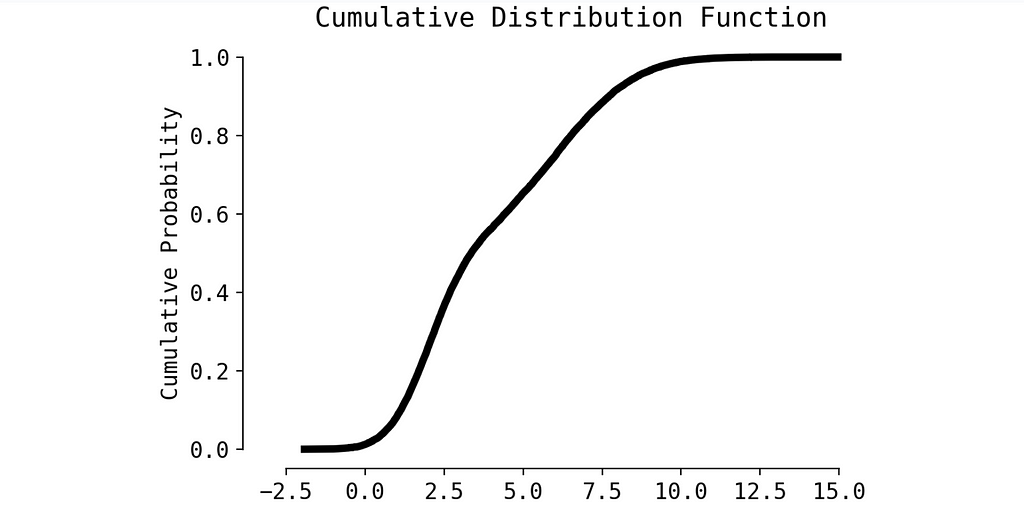
So, we simply need to reconstruct the CDF from the user’s metric, which can be done efficiently using splines. Let’s create a toy example.

Imagine you are an e-commerce platform aiming to personalize your email campaigns based on user activity from the past week. If a user has been less active compared to previous weeks, you plan to send them a discount offer.

You’ve gathered user statistics and noticed the following for a user named John:

• John visited the platform for the first time 15 days ago.
• During the first 7 days (days 1–7), he made 9 visits.
• During the next 7 days (days 2–8), he made 8 visits.
• Totally we have 9 values.

Now, you want to evaluate how extreme the most recent value is compared to the previous ones.

import numpy as np
visits = np.array([9, 8, 6, 5, 8, 6, 8, 7])
num_visits_last_week = 6

Let’s create a CDF of these values.

import numpy as np
import matplotlib.pyplot as plt

values = np.array(sorted(set(visits)))
counts = np.array([data.count(x) for x in values])
probabilities = counts / counts.sum()
cdf = np.cumsum(probabilities)

plt.scatter(values, cdf, color='black', linewidth=10)

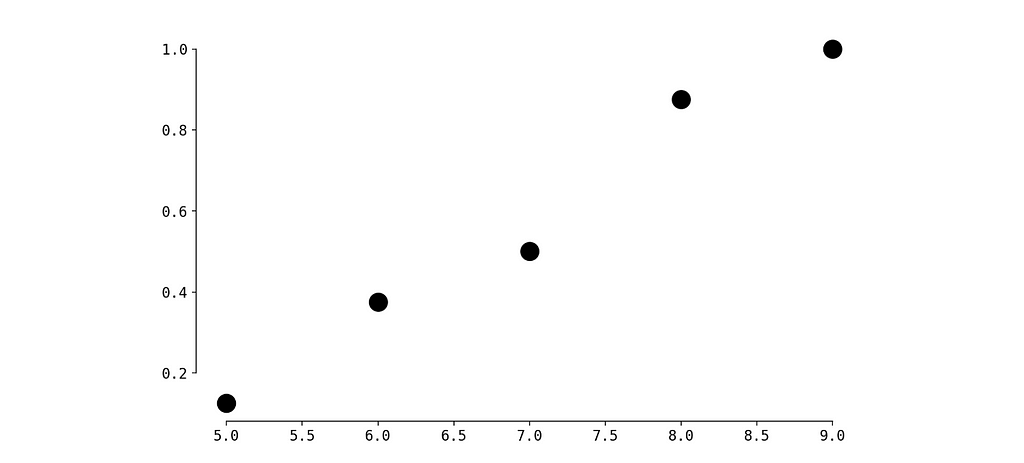
Now we need to restore the function based on these values. We will use spline interpolation.

from scipy.interpolate import make_interp_spline

x_new = np.linspace(values.min(), values.max(), 300)  
spline = make_interp_spline(values, cdf, k=3)         
cdf_smooth = spline(x_new)

plt.plot(x_new, cdf_smooth, label='Сплайн CDF', color='black', linewidth=4)
plt.scatter(values, cdf, color='black', linewidth=10)
plt.scatter(values[-2:], cdf[-2:], color='#f95d5f', linewidth=10, zorder=5)
plt.show()

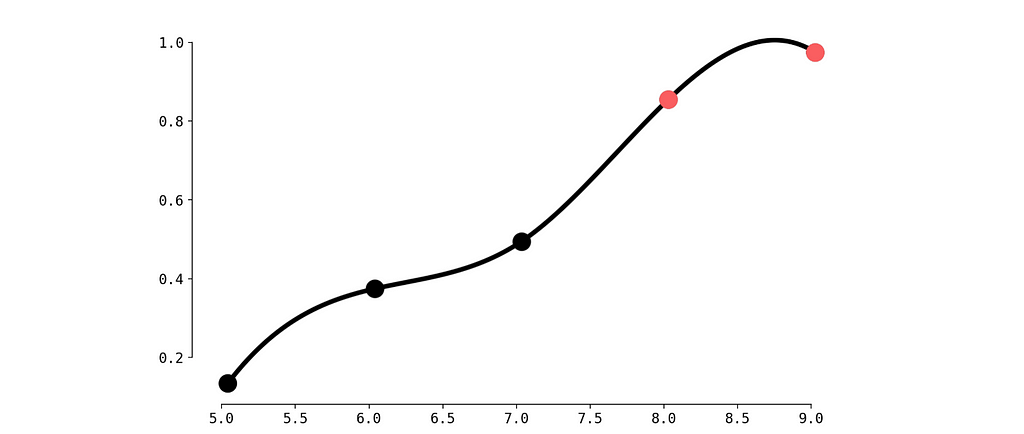
Not bad. But we observe a small problem between red dots — the CDF must be monotonically increasing. Let’s fix this with Piecewise Cubic Hermite Interpolating Polynomial.

from scipy.interpolate import PchipInterpolator

spline_monotonic = PchipInterpolator(values, cdf)
cdf_smooth = spline_monotonic(x_new)

plt.plot(x_new, cdf_smooth, color='black', linewidth=4)
plt.scatter(values, cdf, color='black', linewidth=10) 
plt.show()

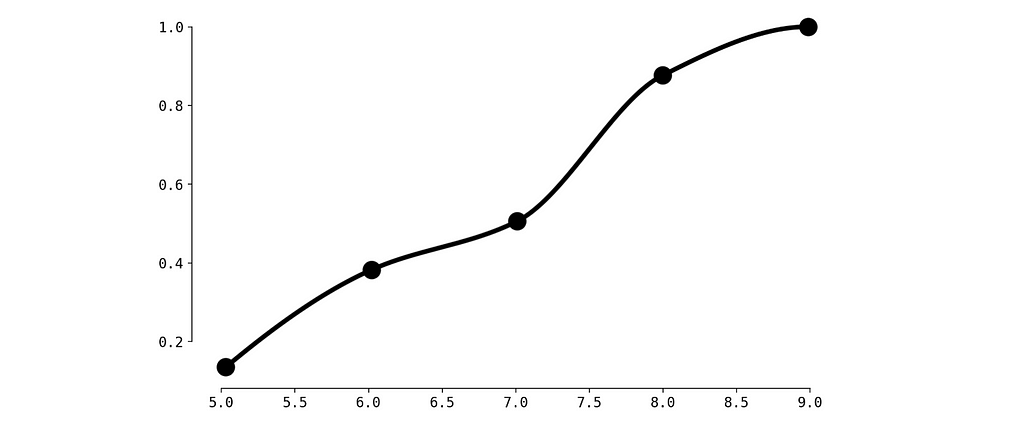
Alright, now it’s perfect.

To calculate p-value for our current observation (6 visits during the last week) we need to calculate the surface of filled area.

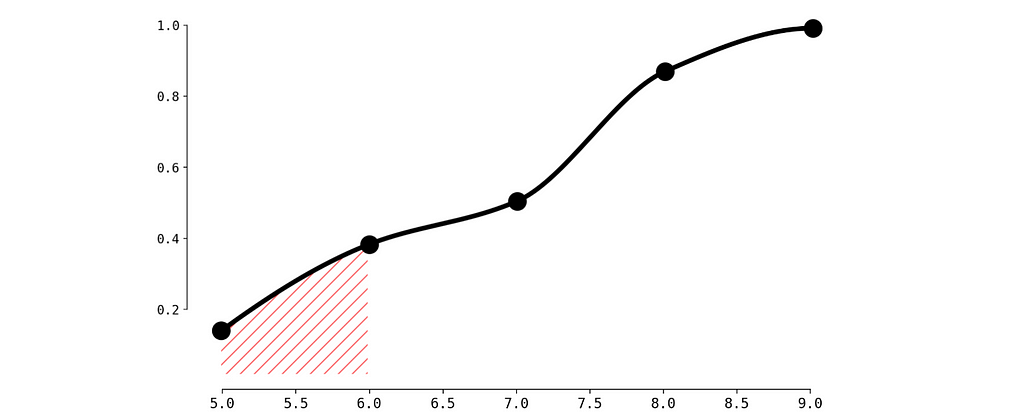
To do so let’s create a simple function calculate_p_value:

def calculate_p_value(x):
    if x < values.min():
        return 0  
    elif x > values.max():
        return 1  
    else:
        return spline_monotonic(x)  

p_value = calculate_p_value(num_visits_last_week)
print(f"Probability of getting less than {num_visits_last_week} equals: {p_value}")

Probability of getting less than 6 equals: 0.375

So the probability is quite high (we may compare it to a threshold 0.1 for instance) and we decide not to send the discount to John. Same calculation we need to do for all the users.

Conclusion

In this article, we have seen how transforming raw user metrics into personalized assessments can lead to more effective business decisions. By using statistical methods like CDF and spline interpolation, we can better understand the context behind user actions and provide personalized, relevant offers that are informed by data.

---

Building Effective Metrics to Describe Users was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.

​How can numerical user metrics, such as “3 visits in the past week,” be transformed into a personalized assessment of whether this behavior is typical or unusual for the user?Cover, image by AuthorIn almost any digital product, analysts often face the challenge of building a digital customer profile — a set of parameters that describe the customer’s state and behavior in one way or another.What are the potential applications of these metrics?Gaining insights into user behaviorLeveraging as features in ML modelsDeveloping business rules for personalized offersA simple example is e-commerce, with metrics like those listed in the table below.Image by AuthorThese metrics are used everywhere, but what is the problem with them? They don’t take into account the specific user’s history or the dynamics of this particular metric. Is $200 spend a lot for user 1? It’s unclear. Yet this distinction significantly influences the business decision we make next.Even within the context of a single user, $200 can have a different meaning for the business depending on the user’s stage in their lifecycle with the product. $200 spent during the user onboarding, pick activity and re-activation are different.User journey, image by AuthorWe’d like to have some normalized metrics to be able compare them between users. Something like this:Image by AuthorSo how can we move from a numerical description of customer behavior to a more characteristic representation? For instance, how can the fact that “a customer hasn’t made a transaction for 7 days” be translated into an individualized assessment of whether this is unusual or typical for that specific customer? The challenge is to achieve this without losing interpretability, preserving business relevance, and avoiding black-box models.A simple approach is to analyze the distribution of the metric and determine the probability of observing the current result (i.e., calculate the p-value). This helps us understand how extreme the value is compared to the user’s history.Normal distribution, image by AuthorBut what’s the challenge here? In most cases, the distribution of metrics is not normal, making p-value calculations more complex.The random metric probably would have a distribution similar to this one:PDF, image by AuthorWe can apply some small trick and to transform Probability Density Function to Cumulative Distribution Function (CDF). Calculating p-value in this case is much easier.CDF, image by AuthorSo, we simply need to reconstruct the CDF from the user’s metric, which can be done efficiently using splines. Let’s create a toy example.Imagine you are an e-commerce platform aiming to personalize your email campaigns based on user activity from the past week. If a user has been less active compared to previous weeks, you plan to send them a discount offer.You’ve gathered user statistics and noticed the following for a user named John:John visited the platform for the first time 15 days ago.During the first 7 days (days 1–7), he made 9 visits.During the next 7 days (days 2–8), he made 8 visits.Totally we have 9 values.Now, you want to evaluate how extreme the most recent value is compared to the previous ones.import numpy as npvisits = np.array([9, 8, 6, 5, 8, 6, 8, 7])num_visits_last_week = 6Let’s create a CDF of these values.import numpy as npimport matplotlib.pyplot as pltvalues = np.array(sorted(set(visits)))counts = np.array([data.count(x) for x in values])probabilities = counts / counts.sum()cdf = np.cumsum(probabilities)plt.scatter(values, cdf, color=’black’, linewidth=10)CDF, image by AuthorNow we need to restore the function based on these values. We will use spline interpolation.from scipy.interpolate import make_interp_splinex_new = np.linspace(values.min(), values.max(), 300) spline = make_interp_spline(values, cdf, k=3) cdf_smooth = spline(x_new)plt.plot(x_new, cdf_smooth, label=’Сплайн CDF’, color=’black’, linewidth=4)plt.scatter(values, cdf, color=’black’, linewidth=10)plt.scatter(values[-2:], cdf[-2:], color=’#f95d5f’, linewidth=10, zorder=5)plt.show()CDF with spline interpolation, image by AuthorNot bad. But we observe a small problem between red dots — the CDF must be monotonically increasing. Let’s fix this with Piecewise Cubic Hermite Interpolating Polynomial.from scipy.interpolate import PchipInterpolatorspline_monotonic = PchipInterpolator(values, cdf)cdf_smooth = spline_monotonic(x_new)plt.plot(x_new, cdf_smooth, color=’black’, linewidth=4)plt.scatter(values, cdf, color=’black’, linewidth=10) plt.show()CDF with Piecewise Cubic Hermite Interpolating, image by AuthorAlright, now it’s perfect.To calculate p-value for our current observation (6 visits during the last week) we need to calculate the surface of filled area.Critical area, image by AuthorTo do so let’s create a simple function calculate_p_value:def calculate_p_value(x): if x < values.min(): return 0 elif x > values.max(): return 1 else: return spline_monotonic(x) p_value = calculate_p_value(num_visits_last_week)print(f”Probability of getting less than {num_visits_last_week} equals: {p_value}”)Probability of getting less than 6 equals: 0.375So the probability is quite high (we may compare it to a threshold 0.1 for instance) and we decide not to send the discount to John. Same calculation we need to do for all the users.ConclusionIn this article, we have seen how transforming raw user metrics into personalized assessments can lead to more effective business decisions. By using statistical methods like CDF and spline interpolation, we can better understand the context behind user actions and provide personalized, relevant offers that are informed by data.Building Effective Metrics to Describe Users was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.  product-management, analytics, user-research, statistics, machine-learning Towards Data Science – MediumRead More

Add to favorites