Investigating an early generative architecture and applying it to image generation from text input
Recently I was tasked with text-to-image synthesis using a conditional variational autoencoder (CVAE). Being one of the earlier generative structures, it has its limitations but is easily implementable. This article will cover CVAEs at a high level, but the reader is presumed to have a high level understanding to cover the applications.
Generative modeling is a field within machine learning focused on learning the underlying distributions responsible for creating data. Understanding these distributions enables models to generalize across various datasets, facilitating knowledge transfer and effectively addressing issues of data sparsity. We ideally want contiguous encodings while still being distinct to allow for smooth interpolation to generate new samples.
Introduction to VAEs
While typical autoencoders are deterministic, VAEs are probabilistic models due to modeling the latent space as a probability distribution. VAEs are unsupervised models that encode input data x into a latent representation z and reconstruct the input from this latent space. They technically don’t need to be implemented with neural networks and can be constructed from generative probability models. However, in our current state of deep learning, most are typically implemented with neural networks.
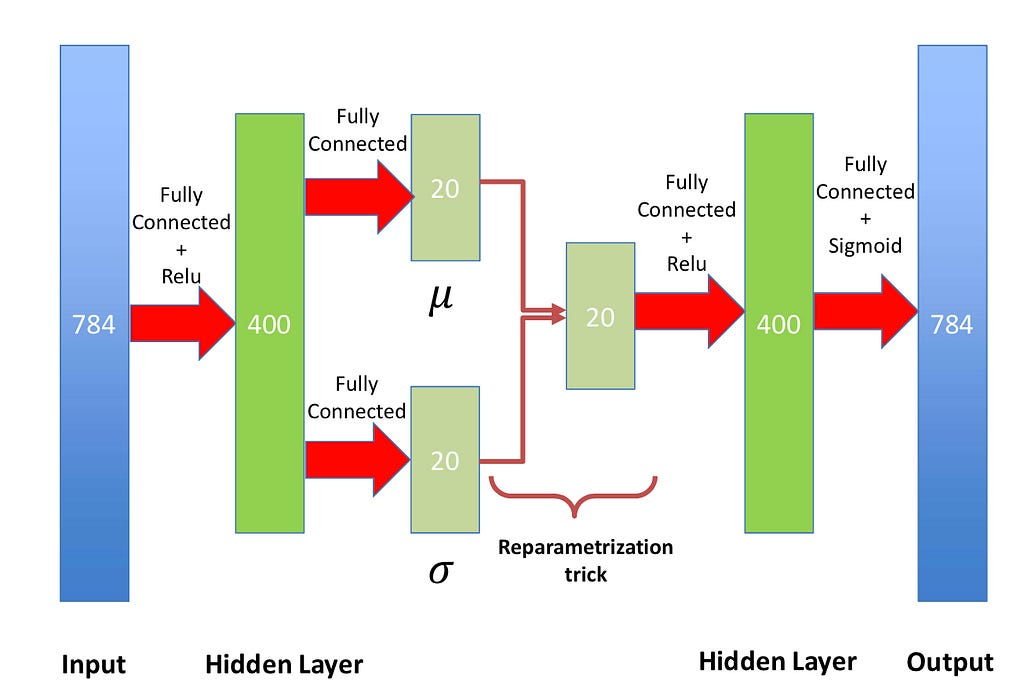
Explained briefly, the reparameterization trick is used since we can’t backpropagate on the probabilistic distribution of the latent space, but we need to update our encoding distribution. Therefore, we define a differentiable and invertible function so that we can differentiate with respect to lambda and x while still keeping a probabilistic element.
VAEs are trained using an ELBO loss consisting of a reconstruction term and a Kullback-Leibler Divergence (KLD) of the encoding model to the prior distribution.
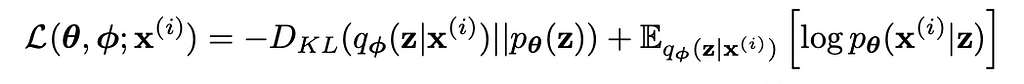
Adding a Conditional Input to VAE
CVAEs extend VAEs by incorporating additional information such as class labels as conditional variables. This conditioning enables CVAEs to produce controlled generations. The conditional input feature can be added at differing points in the architecture, but it is commonly inserted with the encoder and the decoder. The loss function with the conditional input is an adaptation of the ELBO loss in the traditional VAE.
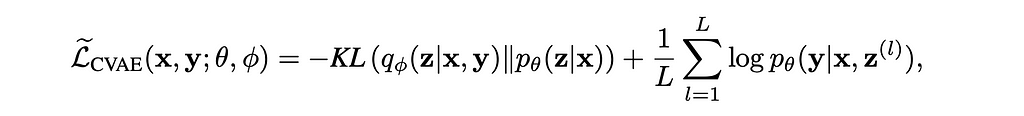
To illustrate the difference between a VAE and CVAE, both networks were trained on Fashion-MNIST using a convolutional encoder and decoder architecture. A tSNE of the latent space of each network is shown.
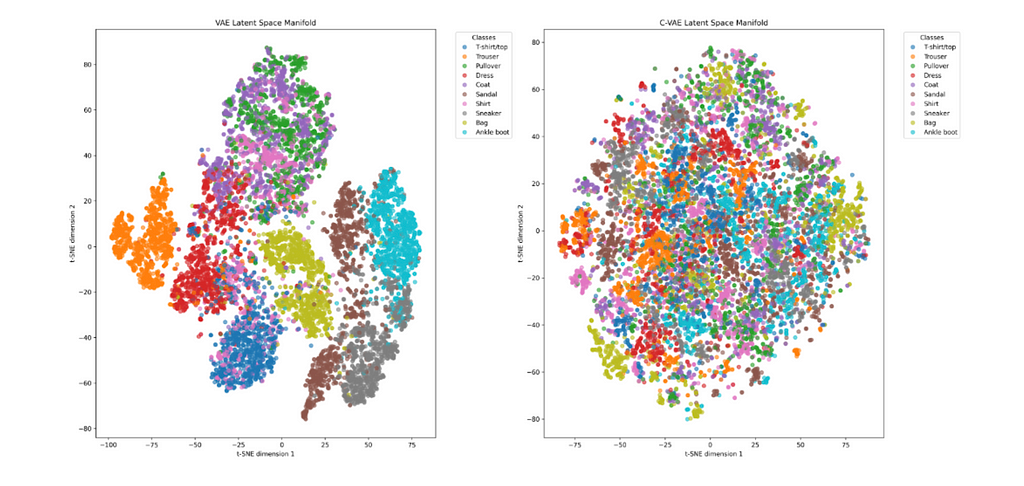
The vanilla VAE shows distinct clusters while the CVAE has a more homogeneous distribution. Vanilla VAE encodes class and class variation into the latent space since there is no provided conditional signal. However, the CVAE does not need to learn class distinction and the latent space can focus on the variation within classes. Therefore, a CVAE can potentially learn more information as it does not rely on having to learn basic class conditioning.
Model Architecture for CVAEs
Two model architectures were created to test image generation. The first architecture was a convolutional CVAE with a concatenating conditional approach. All networks were built for Fashion-MNIST images of size 28×28 (784 total pixels).
class ConcatConditionalVAE(nn.Module):
def __init__(self, latent_dim=128, num_classes=10):
super().__init__()
self.latent_dim = latent_dim
self.num_classes = num_classes
# Encoder
self.encoder = nn.Sequential(
nn.Conv2d(1, 32, 3, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(32, 64, 3, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(64, 128, 3, stride=2, padding=1),
nn.ReLU(),
nn.Flatten()
)
self.flatten_size = 128 * 4 * 4
# Conditional embedding
self.label_embedding = nn.Embedding(num_classes, 32)
# Latent space (with concatenated condition)
self.fc_mu = nn.Linear(self.flatten_size + 32, latent_dim)
self.fc_var = nn.Linear(self.flatten_size + 32, latent_dim)
# Decoder
self.decoder_input = nn.Linear(latent_dim + 32, 4 * 4 * 128)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(128, 64, 2, stride=2, padding=1, output_padding=1),
nn.ReLU(),
nn.ConvTranspose2d(64, 32, 3, stride=2, padding=1, output_padding=1),
nn.ReLU(),
nn.ConvTranspose2d(32, 1, 3, stride=2, padding=1, output_padding=1),
nn.Sigmoid()
)
def encode(self, x, c):
x = self.encoder(x)
c = self.label_embedding(c)
# Concatenate condition with encoded input
x = torch.cat([x, c], dim=1)
mu = self.fc_mu(x)
log_var = self.fc_var(x)
return mu, log_var
def reparameterize(self, mu, log_var):
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z, c):
c = self.label_embedding(c)
# Concatenate condition with latent vector
z = torch.cat([z, c], dim=1)
z = self.decoder_input(z)
z = z.view(-1, 128, 4, 4)
return self.decoder(z)
def forward(self, x, c):
mu, log_var = self.encode(x, c)
z = self.reparameterize(mu, log_var)
return self.decode(z, c), mu, log_var
The CVAE encoder consists of 3 convolutional layers each followed by a ReLU non-linearity. The output of the encoder is then flattened. The class number is then passed through an embedding layer and added to the encoder output. The reparameterization trick is then used with 2 linear layers to obtain a μ and σ in the latent space. Once sampled, the output of the reparameterized latent space is passed to the decoder now concatenated with the class number embedding layer output. The decoder consists of 3 transposed convolutional layers. The first two contain a ReLU non-linearity with the last layer containing a sigmoid non-linearity. The output of the decoder is a 28×28 generated image.
The other model architecture follows the same approach but with adding the conditional input instead of concatenating. A major question was if adding or concatenating will lead to better reconstruction or generation results.
class AdditiveConditionalVAE(nn.Module):
def __init__(self, latent_dim=128, num_classes=10):
super().__init__()
self.latent_dim = latent_dim
self.num_classes = num_classes
# Encoder
self.encoder = nn.Sequential(
nn.Conv2d(1, 32, 3, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(32, 64, 3, stride=2, padding=1),
nn.ReLU(),
nn.Conv2d(64, 128, 3, stride=2, padding=1),
nn.ReLU(),
nn.Flatten()
)
self.flatten_size = 128 * 4 * 4
# Conditional embedding
self.label_embedding = nn.Embedding(num_classes, self.flatten_size)
# Latent space (without concatenation)
self.fc_mu = nn.Linear(self.flatten_size, latent_dim)
self.fc_var = nn.Linear(self.flatten_size, latent_dim)
# Decoder condition embedding
self.decoder_label_embedding = nn.Embedding(num_classes, latent_dim)
# Decoder
self.decoder_input = nn.Linear(latent_dim, 4 * 4 * 128)
self.decoder = nn.Sequential(
nn.ConvTranspose2d(128, 64, 2, stride=2, padding=1, output_padding=1),
nn.ReLU(),
nn.ConvTranspose2d(64, 32, 3, stride=2, padding=1, output_padding=1),
nn.ReLU(),
nn.ConvTranspose2d(32, 1, 3, stride=2, padding=1, output_padding=1),
nn.Sigmoid()
)
def encode(self, x, c):
x = self.encoder(x)
c = self.label_embedding(c)
# Add condition to encoded input
x = x + c
mu = self.fc_mu(x)
log_var = self.fc_var(x)
return mu, log_var
def reparameterize(self, mu, log_var):
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z, c):
# Add condition to latent vector
c = self.decoder_label_embedding(c)
z = z + c
z = self.decoder_input(z)
z = z.view(-1, 128, 4, 4)
return self.decoder(z)
def forward(self, x, c):
mu, log_var = self.encode(x, c)
z = self.reparameterize(mu, log_var)
return self.decode(z, c), mu, log_var
The same loss function is used for all CVAEs from the equation shown above.
def loss_function(recon_x, x, mu, logvar):
"""Computes the loss = -ELBO = Negative Log-Likelihood + KL Divergence.
Args:
recon_x: Decoder output.
x: Ground truth.
mu: Mean of Z
logvar: Log-Variance of Z
"""
BCE = F.binary_cross_entropy(recon_x, x, reduction='sum')
KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return BCE + KLD
In order to assess model-generated images, 3 quantitative metrics are commonly used. Mean Squared Error (MSE) was calculated by summing the squares of the difference between the generated image and a ground truth image pixel-wise. Structural Similarity Index Measure (SSIM) is a metric that evaluates image quality by comparing two images based on structural information, luminance, and contrast [3]. SSIM can be used to compare images of any size while MSE is relative to pixel size. SSIM score ranges from -1 to 1, where 1 indicates identical images. Frechet inception distance (FID) is a metric for quantifying the realism and diversity of images generated. As FID is a distance measure, lower scores are indicative of a better reconstruction of a set of images.
Short Text to Image from Fashion-MNIST
Before scaling up to full text to image, CVAEs image reconstruction and generation on Fashion-MNIST. Fashion-MNIST is an MNIST-like dataset consisting of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28×28 grayscale image, associated with a label from 10 classes [4].
Preprocessing functions were created to extract the relevant key word containing the class name from the input short-text regular expression matching. Extra descriptors (synonyms) were used for most classes to account for similar fashion items included in each class (e.g. Coat & Jacket).
classes = {
'Shirt':0,
'Top':0,
'Trouser':1,
'Pants':1,
'Pullover':2,
'Sweater':2,
'Hoodie':2,
'Dress':3,
'Coat':4,
'Jacket':4,
'Sandal':5,
'Shirt':6,
'Sneaker':7,
'Shoe':7,
'Bag':8,
'Ankle boot':9,
'Boot':9
}
def word_to_text(input_str, classes, model, device):
label = class_embedding(input_str, classes)
if label == -1: return Exception("No valid label")
samples = sample_images(model, num_samples=4, label=label, device=device)
plot_samples(samples, input_str, torch.tensor([label]))
return
def class_embedding(input_str, classes):
for key in list(classes.keys()):
template = f'(?i)\b{key}\b'
output = re.search(template, input_str)
if output: return classes[key]
return -1
The class name was then converted to its class number and used as the conditional input to the CVAE along. In order to generate an image, the class label extracted from the short text description is passed into the decoder with random samples from a Gaussian distribution to input the variable from the latent space.
Before testing generation, image reconstruction is tested to ensure the functionality of the CVAE. Due to creating a convolutional network with 28×28 images, the network can be trained in less than an hour with less than 100 epochs.

Reconstructions contain the general shape of the ground truth images, but sharp, high frequency features are missing from the image. Any text or intricate design patterns are blurred in the model output. Inputting any short text containing a class of Fashion-MNIST gives generated outputs resembling reconstructed images.
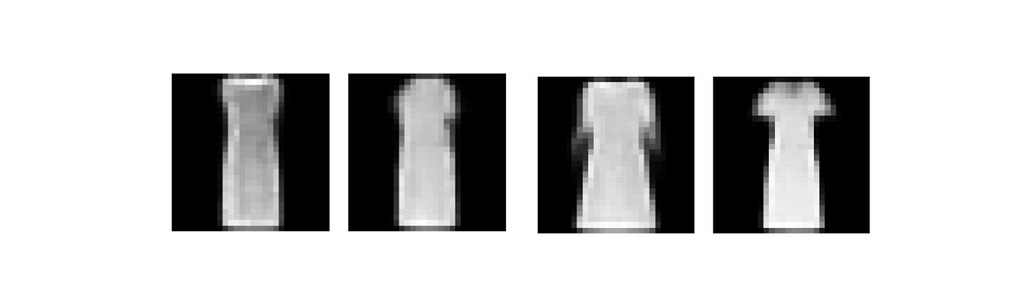
The generated images have an MSE of 11 and a SSIM of 0.76. These constitute good generations signifying that in simple, small images, CVAEs can generate quality images. GANs and DDPMs will produce higher quality images with complex features, but CVAEs can handle simple cases.
Long Text to Image using CLIP and COCO
When scaling up to image generation to text of any length, more robust methods would be needed besides regular expression matching. To do this, Open AI’s CLIP is used to convert text into a high dimensional embedding vector. The embedding model is used in its ViT-B/32 configuration, which outputs embeddings of length 512. A limitation of the CLIP model is that it has a maximum token length of 77, with studies showing an even smaller effective length of 20 [5]. Thus, in instances where the input text contains multiple sentences, the text is split up by sentence and passed through the CLIP encoder. The resulting embeddings are averaged together to create the final output embedding.
A long text model requires far more complicated training data than Fashion-MNIST, so COCO dataset was used. COCO dataset has annotations (that are not completely robust but that will be discussed later) that can be passed into CLIP to get embeddings. However, COCO images are of size 640×480, meaning that even with cropping transforms, a larger network is needed. Adding and concatenating conditional inputs architectures are both tested for long text to image generation, but the concatenating approach is shown here:
class cVAE(nn.Module):
def __init__(self, latent_dim=128):
super().__init__()
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
self.clip_model, _ = clip.load("ViT-B/32", device=device)
self.clip_model.eval()
for param in self.clip_model.parameters():
param.requires_grad = False
self.latent_dim = latent_dim
# Modified encoder for 128x128 input
self.encoder = nn.Sequential(
nn.Conv2d(3, 32, 4, stride=2, padding=1), # 64x64
nn.BatchNorm2d(32),
nn.ReLU(),
nn.Conv2d(32, 64, 4, stride=2, padding=1), # 32x32
nn.BatchNorm2d(64),
nn.ReLU(),
nn.Conv2d(64, 128, 4, stride=2, padding=1), # 16x16
nn.BatchNorm2d(128),
nn.ReLU(),
nn.Conv2d(128, 256, 4, stride=2, padding=1), # 8x8
nn.BatchNorm2d(256),
nn.ReLU(),
nn.Conv2d(256, 512, 4, stride=2, padding=1), # 4x4
nn.BatchNorm2d(512),
nn.ReLU(),
nn.Flatten()
)
self.flatten_size = 512 * 4 * 4 # Flattened size from encoder
# Process CLIP embeddings for encoder
self.condition_processor_encoder = nn.Sequential(
nn.Linear(512, 1024)
)
self.fc_mu = nn.Linear(self.flatten_size + 1024, latent_dim)
self.fc_var = nn.Linear(self.flatten_size + 1024, latent_dim)
self.decoder_input = nn.Linear(latent_dim + 512, 512 * 4 * 4)
# Modified decoder for 128x128 output
self.decoder = nn.Sequential(
nn.ConvTranspose2d(512, 256, 4, stride=2, padding=1), # 8x8
nn.BatchNorm2d(256),
nn.ReLU(),
nn.ConvTranspose2d(256, 128, 4, stride=2, padding=1), # 16x16
nn.BatchNorm2d(128),
nn.ReLU(),
nn.ConvTranspose2d(128, 64, 4, stride=2, padding=1), # 32x32
nn.BatchNorm2d(64),
nn.ReLU(),
nn.ConvTranspose2d(64, 32, 4, stride=2, padding=1), # 64x64
nn.BatchNorm2d(32),
nn.ReLU(),
nn.ConvTranspose2d(32, 16, 4, stride=2, padding=1), # 128x128
nn.BatchNorm2d(16),
nn.ReLU(),
nn.Conv2d(16, 3, 3, stride=1, padding=1), # 128x128
nn.Sigmoid()
)
def encode_condition(self, text):
with torch.no_grad():
embeddings = []
for sentence in text:
embeddings.append(self.clip_model.encode_text(clip.tokenize(sentence).to('cuda')).type(torch.float32))
return torch.mean(torch.stack(embeddings), dim=0)
def encode(self, x, c):
x = self.encoder(x)
c = self.condition_processor_encoder(c)
x = torch.cat([x, c], dim=1)
return self.fc_mu(x), self.fc_var(x)
def reparameterize(self, mu, log_var):
std = torch.exp(0.5 * log_var)
eps = torch.randn_like(std)
return mu + eps * std
def decode(self, z, c):
z = torch.cat([z, c], dim=1)
z = self.decoder_input(z)
z = z.view(-1, 512, 4, 4)
return self.decoder(z)
def forward(self, x, c):
mu, log_var = self.encode(x, c)
z = self.reparameterize(mu, log_var)
return self.decode(z, c), mu, log_var
Another major point of investigation was image generation and reconstruction on images of different sizes. Specifically, modifying COCO images to be of size 64×64, 128×128, and 256×256. After training the network, reconstruction results should first be tested.

All image sizes lead to reconstructed background with some feature outlines and correct colors. However, as image size increases, more features are able to be recovered. This makes sense as although it will take a lot longer to train a model with a larger image size, there is more information that can be captured and learned by the model.
With image generation, it is extremely difficult to generate high quality images. Most images have backgrounds to some degree and blurred features in the image. This would be expected for image generation from a CVAE. This occurs in both concatenation and addition for the conditional input, but the concatenated approach performs better. This is likely because concatenated conditional inputs will not interfere with important features and ensures information is preserved distinctly. Conditions can be ignored if they are irrelevant. However, additive conditional inputs can interfere with existing features and completely mess up the network when updating weights during backpropagation.

All of the COCO generated images have a far lower SSIM of about 0.4 compared to the SSIM on Fashion-MNIST. MSE is proportional to image size, so it is difficult to quanity differences. FID for COCO image generations are in the 200s for further proof that COCO CVAE generated images are not robust.
Limitations of CVAEs for Image Generation
The biggest limitation in trying to use CVAEs for image generation is, well, the CVAE. The amount of information that can be contained and reconstructed/generated is extremely dependent on the size of the latent space. A latent space that is too small won’t capture any meaningful information and is proportional to the size of the output image. A 28×28 image needs a far smaller latent space than a 64×64 image (as it proportionally squares from image size). However, a latent space bigger than the actual image adds unnecessary info and at that point just create a 1-to-1 mapping. For the COCO dataset, a latent space of at least 512 is needed to capture some features. And while CVAEs are generative models, a convolutional encoder and decoder is a rather rudimentary network. The training style of a GAN or the complex denoising process of a DDPM allows for far more complicated image generation.
Another major limitation in image generation is the dataset trained on. Although the COCO dataset has annotations, the annotations are not extensively detailed. In order to train complex generative models, a different dataset should be used for training. COCO does not provide locations or excess information for background details. A complex feature vector from the CLIP encoder can’t be effectively utilized to a CVAE on COCO.
Although CVAEs and image generation on COCO have their limitations, it creates a workable image generation model. More code and details can be provided just reach out!
References
[1] Kingma, Diederik P, et. al. “Auto-encoding variational bayes.” arXiv:1312.6114 (2013).
[2] Sohn, Kihyuk, et. al. “Learning Structured Output Representation using Deep Conditional Generative Models.” NeurIPS Proceedings (2015).
[3] Nilsson, J., et. al. “Understanding ssim.” arXiv:2102.12037 (2020).
[4] Xiao, Han, et. al. “Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms.” arXiv:2403.15378 (2024) (MIT license).
[5] Zhang, B., et. al. “Long-clip: Unlocking the long-text capability of clip.” arXiv:2403.15378 (2024).
A reference to my group project partners Jake Hession (Deloitte Consultant), Ashley Hong (Google SWE), and Julian Kuppel (Quant)!
Conditional Variational Autoencoders for Text to Image Generation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Investigating an early generative architecture and applying it to image generation from text inputRecently I was tasked with text-to-image synthesis using a conditional variational autoencoder (CVAE). Being one of the earlier generative structures, it has its limitations but is easily implementable. This article will cover CVAEs at a high level, but the reader is presumed to have a high level understanding to cover the applications.Generative modeling is a field within machine learning focused on learning the underlying distributions responsible for creating data. Understanding these distributions enables models to generalize across various datasets, facilitating knowledge transfer and effectively addressing issues of data sparsity. We ideally want contiguous encodings while still being distinct to allow for smooth interpolation to generate new samples.Introduction to VAEsWhile typical autoencoders are deterministic, VAEs are probabilistic models due to modeling the latent space as a probability distribution. VAEs are unsupervised models that encode input data x into a latent representation z and reconstruct the input from this latent space. They technically don’t need to be implemented with neural networks and can be constructed from generative probability models. However, in our current state of deep learning, most are typically implemented with neural networks.Example VAE framework with reparameterization trick. Source: AuthorExplained briefly, the reparameterization trick is used since we can’t backpropagate on the probabilistic distribution of the latent space, but we need to update our encoding distribution. Therefore, we define a differentiable and invertible function so that we can differentiate with respect to lambda and x while still keeping a probabilistic element.Reparameterization trick for z. Source: AuthorVAEs are trained using an ELBO loss consisting of a reconstruction term and a Kullback-Leibler Divergence (KLD) of the encoding model to the prior distribution.Loss function for VAE with KLD term on left and reconstruction term on righ [1]Adding a Conditional Input to VAECVAEs extend VAEs by incorporating additional information such as class labels as conditional variables. This conditioning enables CVAEs to produce controlled generations. The conditional input feature can be added at differing points in the architecture, but it is commonly inserted with the encoder and the decoder. The loss function with the conditional input is an adaptation of the ELBO loss in the traditional VAE.Loss function for VAE with KLD term on left and reconstruction term on right [2]To illustrate the difference between a VAE and CVAE, both networks were trained on Fashion-MNIST using a convolutional encoder and decoder architecture. A tSNE of the latent space of each network is shown.Latent space manifold of VAE (left) and CVAE (right). Source: AuthorThe vanilla VAE shows distinct clusters while the CVAE has a more homogeneous distribution. Vanilla VAE encodes class and class variation into the latent space since there is no provided conditional signal. However, the CVAE does not need to learn class distinction and the latent space can focus on the variation within classes. Therefore, a CVAE can potentially learn more information as it does not rely on having to learn basic class conditioning.Model Architecture for CVAEsTwo model architectures were created to test image generation. The first architecture was a convolutional CVAE with a concatenating conditional approach. All networks were built for Fashion-MNIST images of size 28×28 (784 total pixels).class ConcatConditionalVAE(nn.Module): def __init__(self, latent_dim=128, num_classes=10): super().__init__() self.latent_dim = latent_dim self.num_classes = num_classes # Encoder self.encoder = nn.Sequential( nn.Conv2d(1, 32, 3, stride=2, padding=1), nn.ReLU(), nn.Conv2d(32, 64, 3, stride=2, padding=1), nn.ReLU(), nn.Conv2d(64, 128, 3, stride=2, padding=1), nn.ReLU(), nn.Flatten() ) self.flatten_size = 128 * 4 * 4 # Conditional embedding self.label_embedding = nn.Embedding(num_classes, 32) # Latent space (with concatenated condition) self.fc_mu = nn.Linear(self.flatten_size + 32, latent_dim) self.fc_var = nn.Linear(self.flatten_size + 32, latent_dim) # Decoder self.decoder_input = nn.Linear(latent_dim + 32, 4 * 4 * 128) self.decoder = nn.Sequential( nn.ConvTranspose2d(128, 64, 2, stride=2, padding=1, output_padding=1), nn.ReLU(), nn.ConvTranspose2d(64, 32, 3, stride=2, padding=1, output_padding=1), nn.ReLU(), nn.ConvTranspose2d(32, 1, 3, stride=2, padding=1, output_padding=1), nn.Sigmoid() ) def encode(self, x, c): x = self.encoder(x) c = self.label_embedding(c) # Concatenate condition with encoded input x = torch.cat([x, c], dim=1) mu = self.fc_mu(x) log_var = self.fc_var(x) return mu, log_var def reparameterize(self, mu, log_var): std = torch.exp(0.5 * log_var) eps = torch.randn_like(std) return mu + eps * std def decode(self, z, c): c = self.label_embedding(c) # Concatenate condition with latent vector z = torch.cat([z, c], dim=1) z = self.decoder_input(z) z = z.view(-1, 128, 4, 4) return self.decoder(z) def forward(self, x, c): mu, log_var = self.encode(x, c) z = self.reparameterize(mu, log_var) return self.decode(z, c), mu, log_varThe CVAE encoder consists of 3 convolutional layers each followed by a ReLU non-linearity. The output of the encoder is then flattened. The class number is then passed through an embedding layer and added to the encoder output. The reparameterization trick is then used with 2 linear layers to obtain a μ and σ in the latent space. Once sampled, the output of the reparameterized latent space is passed to the decoder now concatenated with the class number embedding layer output. The decoder consists of 3 transposed convolutional layers. The first two contain a ReLU non-linearity with the last layer containing a sigmoid non-linearity. The output of the decoder is a 28×28 generated image.The other model architecture follows the same approach but with adding the conditional input instead of concatenating. A major question was if adding or concatenating will lead to better reconstruction or generation results.class AdditiveConditionalVAE(nn.Module): def __init__(self, latent_dim=128, num_classes=10): super().__init__() self.latent_dim = latent_dim self.num_classes = num_classes # Encoder self.encoder = nn.Sequential( nn.Conv2d(1, 32, 3, stride=2, padding=1), nn.ReLU(), nn.Conv2d(32, 64, 3, stride=2, padding=1), nn.ReLU(), nn.Conv2d(64, 128, 3, stride=2, padding=1), nn.ReLU(), nn.Flatten() ) self.flatten_size = 128 * 4 * 4 # Conditional embedding self.label_embedding = nn.Embedding(num_classes, self.flatten_size) # Latent space (without concatenation) self.fc_mu = nn.Linear(self.flatten_size, latent_dim) self.fc_var = nn.Linear(self.flatten_size, latent_dim) # Decoder condition embedding self.decoder_label_embedding = nn.Embedding(num_classes, latent_dim) # Decoder self.decoder_input = nn.Linear(latent_dim, 4 * 4 * 128) self.decoder = nn.Sequential( nn.ConvTranspose2d(128, 64, 2, stride=2, padding=1, output_padding=1), nn.ReLU(), nn.ConvTranspose2d(64, 32, 3, stride=2, padding=1, output_padding=1), nn.ReLU(), nn.ConvTranspose2d(32, 1, 3, stride=2, padding=1, output_padding=1), nn.Sigmoid() ) def encode(self, x, c): x = self.encoder(x) c = self.label_embedding(c) # Add condition to encoded input x = x + c mu = self.fc_mu(x) log_var = self.fc_var(x) return mu, log_var def reparameterize(self, mu, log_var): std = torch.exp(0.5 * log_var) eps = torch.randn_like(std) return mu + eps * std def decode(self, z, c): # Add condition to latent vector c = self.decoder_label_embedding(c) z = z + c z = self.decoder_input(z) z = z.view(-1, 128, 4, 4) return self.decoder(z) def forward(self, x, c): mu, log_var = self.encode(x, c) z = self.reparameterize(mu, log_var) return self.decode(z, c), mu, log_varThe same loss function is used for all CVAEs from the equation shown above.def loss_function(recon_x, x, mu, logvar): “””Computes the loss = -ELBO = Negative Log-Likelihood + KL Divergence. Args: recon_x: Decoder output. x: Ground truth. mu: Mean of Z logvar: Log-Variance of Z “”” BCE = F.binary_cross_entropy(recon_x, x, reduction=’sum’) KLD = -0.5 * torch.sum(1 + logvar – mu.pow(2) – logvar.exp()) return BCE + KLDIn order to assess model-generated images, 3 quantitative metrics are commonly used. Mean Squared Error (MSE) was calculated by summing the squares of the difference between the generated image and a ground truth image pixel-wise. Structural Similarity Index Measure (SSIM) is a metric that evaluates image quality by comparing two images based on structural information, luminance, and contrast [3]. SSIM can be used to compare images of any size while MSE is relative to pixel size. SSIM score ranges from -1 to 1, where 1 indicates identical images. Frechet inception distance (FID) is a metric for quantifying the realism and diversity of images generated. As FID is a distance measure, lower scores are indicative of a better reconstruction of a set of images.Short Text to Image from Fashion-MNISTBefore scaling up to full text to image, CVAEs image reconstruction and generation on Fashion-MNIST. Fashion-MNIST is an MNIST-like dataset consisting of a training set of 60,000 examples and a test set of 10,000 examples. Each example is a 28×28 grayscale image, associated with a label from 10 classes [4].Preprocessing functions were created to extract the relevant key word containing the class name from the input short-text regular expression matching. Extra descriptors (synonyms) were used for most classes to account for similar fashion items included in each class (e.g. Coat & Jacket).classes = {‘Shirt’:0,’Top’:0,’Trouser’:1,’Pants’:1,’Pullover’:2,’Sweater’:2,’Hoodie’:2,’Dress’:3,’Coat’:4,’Jacket’:4,’Sandal’:5,’Shirt’:6,’Sneaker’:7,’Shoe’:7,’Bag’:8,’Ankle boot’:9,’Boot’:9}def word_to_text(input_str, classes, model, device): label = class_embedding(input_str, classes) if label == -1: return Exception(“No valid label”) samples = sample_images(model, num_samples=4, label=label, device=device) plot_samples(samples, input_str, torch.tensor([label])) returndef class_embedding(input_str, classes): for key in list(classes.keys()): template = f'(?i)\b{key}\b’ output = re.search(template, input_str) if output: return classes[key] return -1The class name was then converted to its class number and used as the conditional input to the CVAE along. In order to generate an image, the class label extracted from the short text description is passed into the decoder with random samples from a Gaussian distribution to input the variable from the latent space.Before testing generation, image reconstruction is tested to ensure the functionality of the CVAE. Due to creating a convolutional network with 28×28 images, the network can be trained in less than an hour with less than 100 epochs.CVAE reconstruction results with ground truth (left) and model output (right). Source: AuthorReconstructions contain the general shape of the ground truth images, but sharp, high frequency features are missing from the image. Any text or intricate design patterns are blurred in the model output. Inputting any short text containing a class of Fashion-MNIST gives generated outputs resembling reconstructed images.Generated images “dress” from CVAE Fashion-MNIST. Source: AuthorThe generated images have an MSE of 11 and a SSIM of 0.76. These constitute good generations signifying that in simple, small images, CVAEs can generate quality images. GANs and DDPMs will produce higher quality images with complex features, but CVAEs can handle simple cases.Long Text to Image using CLIP and COCOWhen scaling up to image generation to text of any length, more robust methods would be needed besides regular expression matching. To do this, Open AI’s CLIP is used to convert text into a high dimensional embedding vector. The embedding model is used in its ViT-B/32 configuration, which outputs embeddings of length 512. A limitation of the CLIP model is that it has a maximum token length of 77, with studies showing an even smaller effective length of 20 [5]. Thus, in instances where the input text contains multiple sentences, the text is split up by sentence and passed through the CLIP encoder. The resulting embeddings are averaged together to create the final output embedding.A long text model requires far more complicated training data than Fashion-MNIST, so COCO dataset was used. COCO dataset has annotations (that are not completely robust but that will be discussed later) that can be passed into CLIP to get embeddings. However, COCO images are of size 640×480, meaning that even with cropping transforms, a larger network is needed. Adding and concatenating conditional inputs architectures are both tested for long text to image generation, but the concatenating approach is shown here:class cVAE(nn.Module): def __init__(self, latent_dim=128): super().__init__() device = torch.device(“cuda” if torch.cuda.is_available() else “cpu”) self.clip_model, _ = clip.load(“ViT-B/32”, device=device) self.clip_model.eval() for param in self.clip_model.parameters(): param.requires_grad = False self.latent_dim = latent_dim # Modified encoder for 128×128 input self.encoder = nn.Sequential( nn.Conv2d(3, 32, 4, stride=2, padding=1), # 64×64 nn.BatchNorm2d(32), nn.ReLU(), nn.Conv2d(32, 64, 4, stride=2, padding=1), # 32×32 nn.BatchNorm2d(64), nn.ReLU(), nn.Conv2d(64, 128, 4, stride=2, padding=1), # 16×16 nn.BatchNorm2d(128), nn.ReLU(), nn.Conv2d(128, 256, 4, stride=2, padding=1), # 8×8 nn.BatchNorm2d(256), nn.ReLU(), nn.Conv2d(256, 512, 4, stride=2, padding=1), # 4×4 nn.BatchNorm2d(512), nn.ReLU(), nn.Flatten() ) self.flatten_size = 512 * 4 * 4 # Flattened size from encoder # Process CLIP embeddings for encoder self.condition_processor_encoder = nn.Sequential( nn.Linear(512, 1024) ) self.fc_mu = nn.Linear(self.flatten_size + 1024, latent_dim) self.fc_var = nn.Linear(self.flatten_size + 1024, latent_dim) self.decoder_input = nn.Linear(latent_dim + 512, 512 * 4 * 4) # Modified decoder for 128×128 output self.decoder = nn.Sequential( nn.ConvTranspose2d(512, 256, 4, stride=2, padding=1), # 8×8 nn.BatchNorm2d(256), nn.ReLU(), nn.ConvTranspose2d(256, 128, 4, stride=2, padding=1), # 16×16 nn.BatchNorm2d(128), nn.ReLU(), nn.ConvTranspose2d(128, 64, 4, stride=2, padding=1), # 32×32 nn.BatchNorm2d(64), nn.ReLU(), nn.ConvTranspose2d(64, 32, 4, stride=2, padding=1), # 64×64 nn.BatchNorm2d(32), nn.ReLU(), nn.ConvTranspose2d(32, 16, 4, stride=2, padding=1), # 128×128 nn.BatchNorm2d(16), nn.ReLU(), nn.Conv2d(16, 3, 3, stride=1, padding=1), # 128×128 nn.Sigmoid() ) def encode_condition(self, text): with torch.no_grad(): embeddings = [] for sentence in text: embeddings.append(self.clip_model.encode_text(clip.tokenize(sentence).to(‘cuda’)).type(torch.float32)) return torch.mean(torch.stack(embeddings), dim=0) def encode(self, x, c): x = self.encoder(x) c = self.condition_processor_encoder(c) x = torch.cat([x, c], dim=1) return self.fc_mu(x), self.fc_var(x) def reparameterize(self, mu, log_var): std = torch.exp(0.5 * log_var) eps = torch.randn_like(std) return mu + eps * std def decode(self, z, c): z = torch.cat([z, c], dim=1) z = self.decoder_input(z) z = z.view(-1, 512, 4, 4) return self.decoder(z) def forward(self, x, c): mu, log_var = self.encode(x, c) z = self.reparameterize(mu, log_var) return self.decode(z, c), mu, log_varAnother major point of investigation was image generation and reconstruction on images of different sizes. Specifically, modifying COCO images to be of size 64×64, 128×128, and 256×256. After training the network, reconstruction results should first be tested.CVAE reconstruction on COCO with different image sizes. Source: AuthorAll image sizes lead to reconstructed background with some feature outlines and correct colors. However, as image size increases, more features are able to be recovered. This makes sense as although it will take a lot longer to train a model with a larger image size, there is more information that can be captured and learned by the model.With image generation, it is extremely difficult to generate high quality images. Most images have backgrounds to some degree and blurred features in the image. This would be expected for image generation from a CVAE. This occurs in both concatenation and addition for the conditional input, but the concatenated approach performs better. This is likely because concatenated conditional inputs will not interfere with important features and ensures information is preserved distinctly. Conditions can be ignored if they are irrelevant. However, additive conditional inputs can interfere with existing features and completely mess up the network when updating weights during backpropagation.Generated images by CVAE on COCO. Source: AuthorAll of the COCO generated images have a far lower SSIM of about 0.4 compared to the SSIM on Fashion-MNIST. MSE is proportional to image size, so it is difficult to quanity differences. FID for COCO image generations are in the 200s for further proof that COCO CVAE generated images are not robust.Limitations of CVAEs for Image GenerationThe biggest limitation in trying to use CVAEs for image generation is, well, the CVAE. The amount of information that can be contained and reconstructed/generated is extremely dependent on the size of the latent space. A latent space that is too small won’t capture any meaningful information and is proportional to the size of the output image. A 28×28 image needs a far smaller latent space than a 64×64 image (as it proportionally squares from image size). However, a latent space bigger than the actual image adds unnecessary info and at that point just create a 1-to-1 mapping. For the COCO dataset, a latent space of at least 512 is needed to capture some features. And while CVAEs are generative models, a convolutional encoder and decoder is a rather rudimentary network. The training style of a GAN or the complex denoising process of a DDPM allows for far more complicated image generation.Another major limitation in image generation is the dataset trained on. Although the COCO dataset has annotations, the annotations are not extensively detailed. In order to train complex generative models, a different dataset should be used for training. COCO does not provide locations or excess information for background details. A complex feature vector from the CLIP encoder can’t be effectively utilized to a CVAE on COCO.Although CVAEs and image generation on COCO have their limitations, it creates a workable image generation model. More code and details can be provided just reach out!References[1] Kingma, Diederik P, et. al. “Auto-encoding variational bayes.” arXiv:1312.6114 (2013).[2] Sohn, Kihyuk, et. al. “Learning Structured Output Representation using Deep Conditional Generative Models.” NeurIPS Proceedings (2015).[3] Nilsson, J., et. al. “Understanding ssim.” arXiv:2102.12037 (2020).[4] Xiao, Han, et. al. “Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms.” arXiv:2403.15378 (2024) (MIT license).[5] Zhang, B., et. al. “Long-clip: Unlocking the long-text capability of clip.” arXiv:2403.15378 (2024).A reference to my group project partners Jake Hession (Deloitte Consultant), Ashley Hong (Google SWE), and Julian Kuppel (Quant)!Conditional Variational Autoencoders for Text to Image Generation was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story. hands-on-tutorials, variational-autoencoder, computer-vision, deep-learning, machine-learning Towards Data Science – MediumRead More

 Add to favorites
Add to favorites


0 Comments