Predictive and prescriptive analytics to bridge the gap between segmentation and prediction for real-world applications

Introduction:
In many real-world machine learning tasks, the population being studied is often diverse and heterogeneous. This variability presents unique challenges, particularly in regression and classification tasks where a single, generalized model may fail to capture important nuances within the data. For example, segmenting customers in marketing campaigns, estimating the sales of a new product using data from comparable products, or diagnosing a patient with limited medical history based on similar cases all highlight the need for models that can adapt to different subpopulations.
This concept of segmentation is not new. Models like k-Nearest Neighbors or Decision Trees already implicitly leverage the idea of dividing the input space into regions that share somewhat similar properties. However, these approaches are often heuristic and do not explicitly optimize for both clustering and prediction simultaneously.
In this article, we approach this challenge from an optimization perspective, following the literature on Predictive and Prescriptive Analytics ([8]). Specifically, we focus on the task of joint clustering and prediction, which seeks to segment the data into clusters while simultaneously fitting a predictive model within each cluster. This approach has gained attention for its ability to bridge the gap between data-driven decision-making and actionable insights and extracting more information from data than other traditional methods (see [2] for instance).
After presenting some theoretical insights on Clustering and Regression from recent literature, we introduce a novel Classification method (Cluster While Classify) and show its superior performance in low data environments.
1. Joint Clustering and Regression
1.1 Original optimization problem
We first start with formulating the problem of optimal clustering and regression — jointly — to achieve the best fitting and prediction performance. Some formal notations and assumptions:
- Data has the form (X, Y), where X = (xᵢ) are the features and Y is the target.
- We assume a clustering with k clusters — k can be defined later — and introduce the binary variables zᵢⱼ equal to 1 if the i-th data point is assigned to cluster j, 0 otherwise.
- We assume a class of regression models (fⱼ) (e.g. linear models), parametrized by (θⱼ) and their loss function L. Note that each θⱼ is specific to regression model fⱼ.
As ultimately a regression problem, the goal of the task is to find the set of parameters (i.e. parameters for each regression model θⱼ as well as the additional cluster assignment variables zᵢⱼ) minimizing the loss function L:
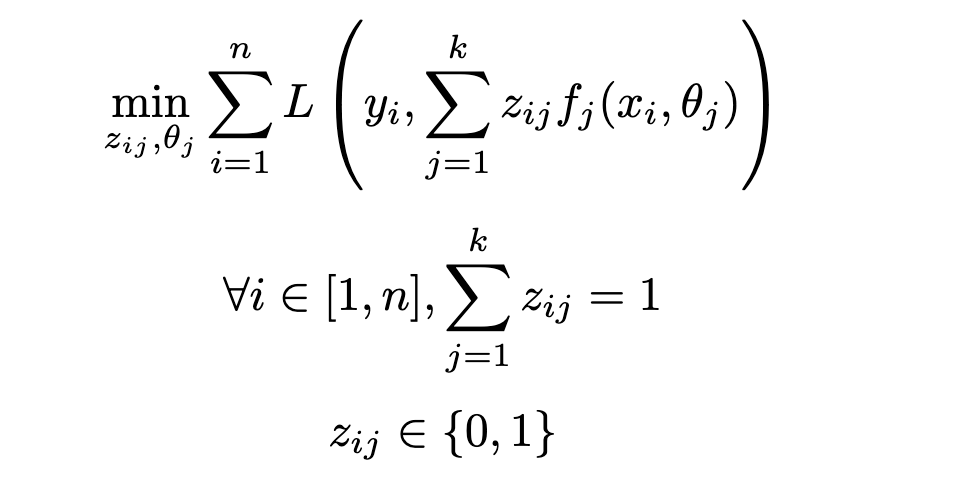
1.2 Suboptimality of Cluster Then Regress:
One of the most natural approaches — and used in numerous practical application of clustering and regression analyses — is the naive Cluster Then Regress (CTR) approach — i.e. first running clustering then run a regression model on the static result of this clustering. It is known to be suboptimal: namely, error propagates from the clustering step to the regression step, and erroneous assignments can have significant consequences on the performance.
We will mathematically show this suboptimality. When running a CTR approach, we first assign the clusters, and then fit the k regression models with cluster assignments as static. This translates to the following nested optimization:
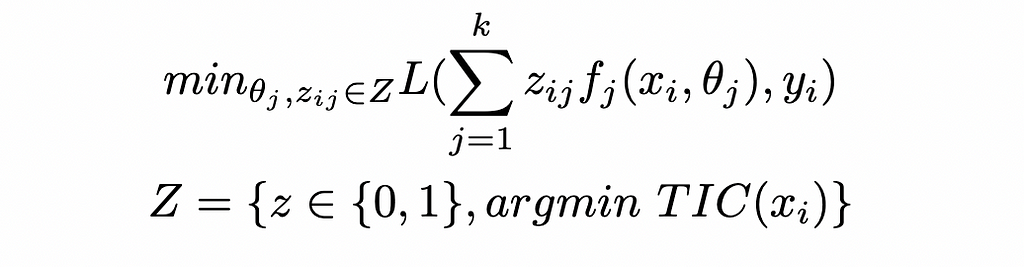
With TIC a measure of Total Intra Cluster Variance. Given that Z is included in ({0, 1})ⁿ, we see that the CTR approach solves a problem that is actually more constrained the the original one (i.e. further constraining the (zᵢⱼ) to be in Z rather than free in ({0, 1})ⁿ). Consequently, this yields a suboptimal result for the original optimization.
1.3 Cluster While Regress: an approximation solution to the original optimization
Unfortunately, attempting to directly solve the original optimization presented in section 1.1 can be intractable in practice, (Mixed integer optimization problem, with potential non-linearity coming from the choice of regression models). [1] presents a fast and easy — but approximate — solution to jointly learn the optimal cluster assignment and regression models: doing it iteratively. In practice, the Cluster While Regress (CWR) is:
- At iteration i, consider cluster assignments as static and calibrate the k regression models
- Then consider the regression models as static and choose the cluster assignments that would minimize the total loss
- Redo the previous two steps until cluster assignments do not change
Besides the iterative nature of this method, it presents a key difference with the CTR approach: clustering and regression optimize for the same objective function.
2. Joint Clustering and Classification
Applying the previous reasoning to classification, we have 2 different routes:
- Rewriting a new model from scratch, i.e. Cluster While Classify
- Using CWR on the log odds for a Logistic Regression approach — see appendix
2.1 Formulating Cluster While Classify:
A few modifications are to be done to the objective problem, namely the loss function L which becomes a classification loss. For simplicity, we will focus on binary classification, but this formulation can easily be extended.
A popular loss function when doing binary classification is the binary cross-entropy loss:
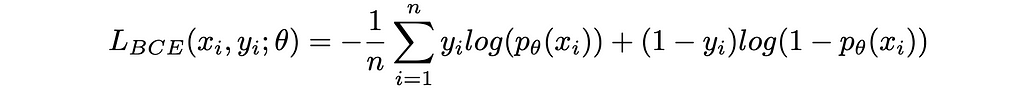
Where p is the prediction of the classification model parametrized by θ in terms of probability of being in the class 1.
Introducing the clustering into this loss yields the following optimization model:
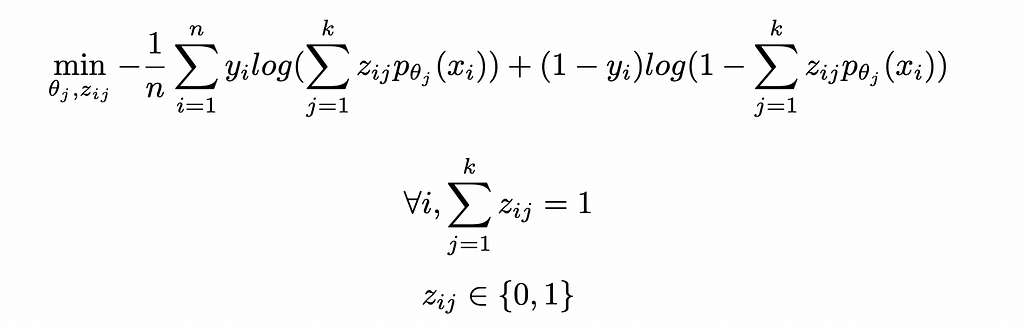
Similarly to CWR, we can find an approximate solution to this problem through the same algorithm, i.e. iteratively fitting the clustering and classification steps until convergence.
2.2. Application for Logistic Regression:
In this specific case, the probabilities are of the form:
Injecting this formula in the objective function of the optimization problem gives:

2.3 Model inference:
Inference with both CWR and CWC models can be done with the following process, described in details in [1]:
- Infer cluster assignment: fit a multiclass classification model on the data points with labels being the final cluster assignments. Use this classification model to assign probabilities of being in a cluster.
- Prediction: for a given data point, the probability of being in a given class becomes the weighted sum of probabilities given by each fitted model. This comes from the law of total probability:
Where P(Yᵢ = 1| Xᵢ, i ∈ Clusterⱼ) is given by j-th classification model fitted and P(i ∈ Clusterⱼ) comes from the cluster assignment classifier.
3. Generalization to non-integer weights
Generalization to non-integer weights relaxes the integer constraint on the z variables. This corresponds to the case of an algorithm allowing for (probabilistic) assignment to multiple clusters, e.g. Soft K-Means — in this case assignments become weights between 0 and 1.
The fitting and inference processes are very similar to previously, with the sole differences being during the fitting phase: calibrating the regression / classification models on each cluster is replaced with calibrated the weighted regressions (e.g. Weighted Least Squares) or weighted classifications (e.g. Weighted Logistic Regression — see [4] for an example), with weight matrices Wⱼ = Diag(zᵢⱼ) with i corresponding to all the indices such that zᵢⱼ > 0. Note that unlike methods such as Weighted Least Squares, weights here are given when fitting the regression.
This generalization has 2 direct implications on the problem at hand:
- Being a less constrained optimization problem, it will naturally yield a better solution, i.e. a lower loss in-sample than the integer-constrained version
- It will be more prone to overfitting, therefore bringing the need for increased regularization
[1] already included a regularization term for the regression coefficients, which corresponds to having regularized fⱼ models: in the case of a Linear Regression, this would means for instance that fⱼ is a LASSO or a Ridge rather than a simple OLS.
Yet, the proposal here is different, as we suggest additional regularization, this time penalizing the non-zero zᵢⱼ: the rationale is that we want to limit the number of models implicated in the fitting / inference of a given data point to reduce noise and degrees of freedom to prevent overfitting.
In practice, we add a new set of binary variables (bᵢⱼ) equal to 1 if zᵢⱼ > 0 and 0 otherwise. We can write it as linear constraints using the big M method:
All in, we have the two optimization models:
Generalized Cluster While Regress:
Generalized Cluster While Classify:
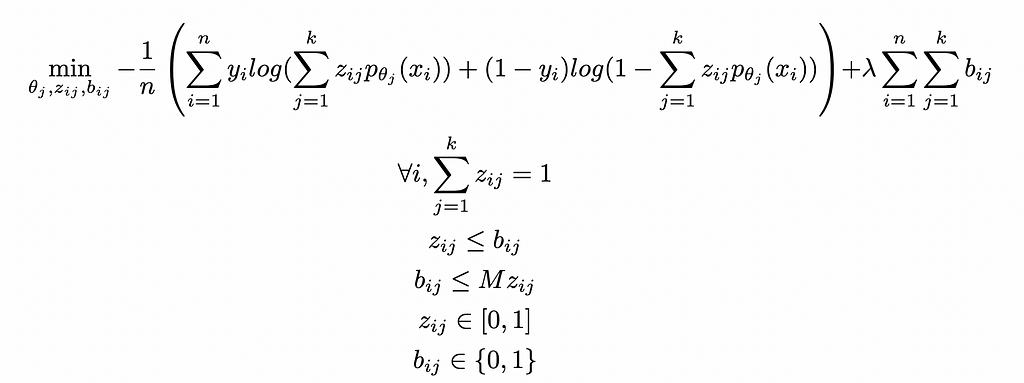
These problems can be efficiently solved with First Order methods or Cutting Planes — see [3] for details.
4. Evaluation:
We evaluate these methods on 3 different benchmark datasets to illustrate 3 key aspects of their behavior and performance:
- Propension to overfit
- Better performance when data is imbalanced or asymmetric — i.e. bigger consequences in cases of false positive or false negative
- Better performance in low data settings
Some implementation details:
- Given that all the methods presented are agnostic to the type of classification model used, we will assume the same classifier across the board to ensure fair comparison. For simplicity, we choose Logistic Regression with L2 regularization (which is the base setting in Scikit-Learn).
- For Cluster Then Classify (CTC), we use the K-Means clustering algorithm. We choose the number of clusters that maximizes the silhouette score of the clustering.
- For Cluster While Classify (CWC), we choose the number of clusters by cross-validation, i.e. the number of clusters that maximizes the AUC of the ROC curve on a validation dataset. We then re-fit the chosen model on both train and validation datasets. If the optimal number of clusters is 2, we opt for the CWC with integer weights for parsimony.
- Inference for CTC and CWC is done with using process Model Inference presented earlier, i.e. a weighted sum of the probabilities predicted by each sub-model.
4.1 UCI Diabetes 130 dataset
The Diabetes 130-US Hospitals dataset (1999–2008) ([5]) contains information about diabetes patients admitted to 130 hospitals across the United States over a 9-year period. The goal of the classification task is to predict whether a given diabetes patient will be readmitted. We will simplify the classes into 2 classes — readmitted or not — instead of 3 (readmitted after less than 30 days, readmitted after more than 30 days, not readmitted). We will also consider a subset of 20,000 data points instead of the full 100,000 instances for faster training.

4.2 UCI MAGIC Gamma Telescope dataset
The MAGIC Gamma Telescope dataset ([6]) contains data from an observatory aimed at classifying high-energy cosmic ray events as either gamma rays (signal) or hadrons (background). A specificity of this dataset is the non-symmetric nature of errors: given the higher cost of false positives (misclassifying hadrons as gamma rays), accuracy is not suitable. Instead, performance is evaluated using the ROC curve and AUC, with a focus on maintaining a false positive rate (FPR) below 20% — as explained in [6].

4.3 UCI Parkinsons dataset
The Parkinson’s dataset ([7]) contains data collected from voice recordings of 195 individuals, including both those with Parkinson’s disease and healthy controls. The dataset is used for classifying the presence or absence of Parkinson’s based on features extracted from speech signals. A key challenge of this dataset is the low number of datapoints, which makes generalization with traditional ML methods difficult. We can diagnose this generalization challenge and overfitting by comparing the performance numbers on train vs test sets.

Conclusion
The study of baseline and joint clustering and classification approaches demonstrates that choice of method depends significantly on the characteristics of the data and the problem setting — in short, there is no one-size-fits-all model.
Our findings highlight key distinctions between the approaches studied across various scenarios:
- In traditional settings, i.e. large datasets, numerous features and balanced outcomes, conventional machine learning models generally perform well. The added step of clustering offers minor benefits, but the potential for overfitting with methods like CWC may lead to worse performance on unseen data.
- In non-traditional settings with asymmetric error consequences, where false positives or false negatives carry unequal costs, methods like CWC provide some advantage. By tailoring predictions to cluster-specific dynamics, CWC seems to better aligns with the loss function’s priorities.
- In low-data environments, the benefits of joint clustering and prediction become particularly pronounced. While traditional models and CTC approaches often struggle with overfitting due to insufficient data, CWC outperforms by extracting more information from what is available. Its iterative optimization framework enables better generalization and robustness in these challenging scenarios.
Appendix:
CWR on the log odds for Logistic Regression
Starting with the log odds of Logistic Regression in the CWR form:
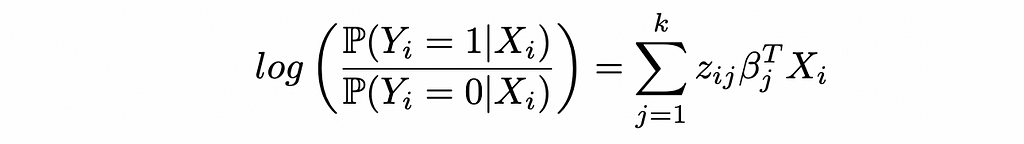
This yields the probabilities:
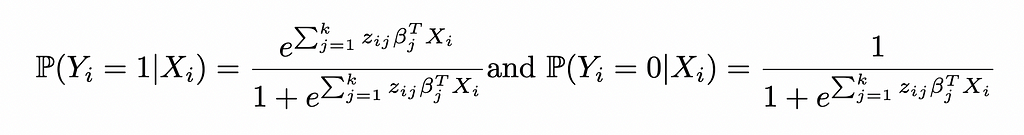
Reinjecting these expressions in the likelihood function of Logistic Regression:
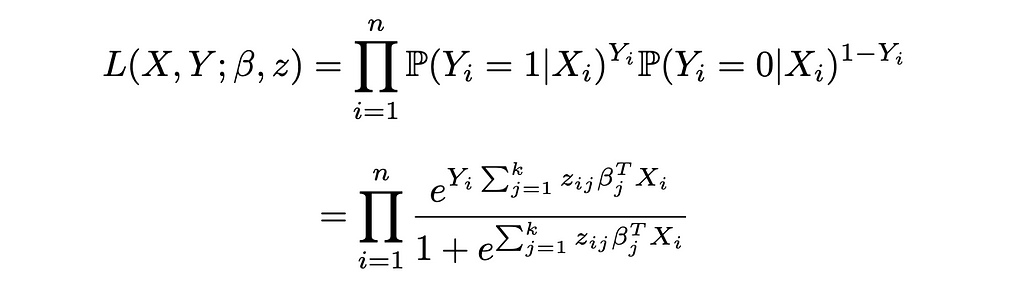
And the log-likelihood:
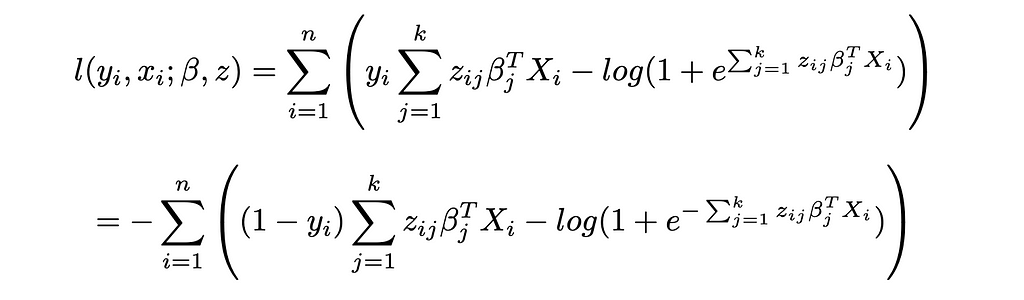
This yields the same objective function as CWC when constraining the zᵢⱼ to be binary variables.
References:
[1] L. Baardman, I. Levin, G. Perakis, D. Singhvi, Leveraging Comparables for New Product Sales Forecasting (2018), Wiley
[2] L. Baardman, R. Cristian, G. Perakis, D. Singhvi, O. Skali Lami, L. Thayaparan, The role of optimization in some recent advances in data-driven decision-making (2023), Springer Nature
[3] D. Bertsimas, J. Dunn, Machine Learning Under a Modern Optimization Lens (2021), Dynamic Ideas
[4] G. Zeng, A comprehensive study of coefficient signs in weighted logistic regression (2024), Helyion
[5] J. Clore, K. Cios, J. DeShazo, B. Strack, Diabetes 130-US Hospitals for Years 1999–2008 [Dataset] (2014), UCI Machine Learning Repository (CC BY 4.0)
[6] R. Bock, MAGIC Gamma Telescope [Dataset] (2004), UCI Machine Learning Repository (CC BY 4.0)
[7] M. Little, Parkinsons [Dataset] (2007). UCI Machine Learning Repository (CC BY 4.0)
[8] D. Bertsimas, N. Kallus, From Predictive to Prescriptive Analytics (2019), INFORMS
Cluster While Predict: Iterative Methods for Regression and Classification was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story.
Predictive and prescriptive analytics to bridge the gap between segmentation and prediction for real-world applicationsPhoto by NASA Hubble Space Telescope on UnsplashIntroduction:In many real-world machine learning tasks, the population being studied is often diverse and heterogeneous. This variability presents unique challenges, particularly in regression and classification tasks where a single, generalized model may fail to capture important nuances within the data. For example, segmenting customers in marketing campaigns, estimating the sales of a new product using data from comparable products, or diagnosing a patient with limited medical history based on similar cases all highlight the need for models that can adapt to different subpopulations.This concept of segmentation is not new. Models like k-Nearest Neighbors or Decision Trees already implicitly leverage the idea of dividing the input space into regions that share somewhat similar properties. However, these approaches are often heuristic and do not explicitly optimize for both clustering and prediction simultaneously.In this article, we approach this challenge from an optimization perspective, following the literature on Predictive and Prescriptive Analytics ([8]). Specifically, we focus on the task of joint clustering and prediction, which seeks to segment the data into clusters while simultaneously fitting a predictive model within each cluster. This approach has gained attention for its ability to bridge the gap between data-driven decision-making and actionable insights and extracting more information from data than other traditional methods (see [2] for instance).After presenting some theoretical insights on Clustering and Regression from recent literature, we introduce a novel Classification method (Cluster While Classify) and show its superior performance in low data environments.1. Joint Clustering and Regression1.1 Original optimization problemWe first start with formulating the problem of optimal clustering and regression — jointly — to achieve the best fitting and prediction performance. Some formal notations and assumptions:Data has the form (X, Y), where X = (xᵢ) are the features and Y is the target.We assume a clustering with k clusters — k can be defined later — and introduce the binary variables zᵢⱼ equal to 1 if the i-th data point is assigned to cluster j, 0 otherwise.We assume a class of regression models (fⱼ) (e.g. linear models), parametrized by (θⱼ) and their loss function L. Note that each θⱼ is specific to regression model fⱼ.As ultimately a regression problem, the goal of the task is to find the set of parameters (i.e. parameters for each regression model θⱼ as well as the additional cluster assignment variables zᵢⱼ) minimizing the loss function L:1.2 Suboptimality of Cluster Then Regress:One of the most natural approaches — and used in numerous practical application of clustering and regression analyses — is the naive Cluster Then Regress (CTR) approach — i.e. first running clustering then run a regression model on the static result of this clustering. It is known to be suboptimal: namely, error propagates from the clustering step to the regression step, and erroneous assignments can have significant consequences on the performance.We will mathematically show this suboptimality. When running a CTR approach, we first assign the clusters, and then fit the k regression models with cluster assignments as static. This translates to the following nested optimization:With TIC a measure of Total Intra Cluster Variance. Given that Z is included in ({0, 1})ⁿ, we see that the CTR approach solves a problem that is actually more constrained the the original one (i.e. further constraining the (zᵢⱼ) to be in Z rather than free in ({0, 1})ⁿ). Consequently, this yields a suboptimal result for the original optimization.1.3 Cluster While Regress: an approximation solution to the original optimizationUnfortunately, attempting to directly solve the original optimization presented in section 1.1 can be intractable in practice, (Mixed integer optimization problem, with potential non-linearity coming from the choice of regression models). [1] presents a fast and easy — but approximate — solution to jointly learn the optimal cluster assignment and regression models: doing it iteratively. In practice, the Cluster While Regress (CWR) is:At iteration i, consider cluster assignments as static and calibrate the k regression modelsThen consider the regression models as static and choose the cluster assignments that would minimize the total lossRedo the previous two steps until cluster assignments do not changeBesides the iterative nature of this method, it presents a key difference with the CTR approach: clustering and regression optimize for the same objective function.2. Joint Clustering and ClassificationApplying the previous reasoning to classification, we have 2 different routes:Rewriting a new model from scratch, i.e. Cluster While ClassifyUsing CWR on the log odds for a Logistic Regression approach — see appendix2.1 Formulating Cluster While Classify:A few modifications are to be done to the objective problem, namely the loss function L which becomes a classification loss. For simplicity, we will focus on binary classification, but this formulation can easily be extended.A popular loss function when doing binary classification is the binary cross-entropy loss:Where p is the prediction of the classification model parametrized by θ in terms of probability of being in the class 1.Introducing the clustering into this loss yields the following optimization model:Similarly to CWR, we can find an approximate solution to this problem through the same algorithm, i.e. iteratively fitting the clustering and classification steps until convergence.2.2. Application for Logistic Regression:In this specific case, the probabilities are of the form:Injecting this formula in the objective function of the optimization problem gives:2.3 Model inference:Inference with both CWR and CWC models can be done with the following process, described in details in [1]:Infer cluster assignment: fit a multiclass classification model on the data points with labels being the final cluster assignments. Use this classification model to assign probabilities of being in a cluster.Prediction: for a given data point, the probability of being in a given class becomes the weighted sum of probabilities given by each fitted model. This comes from the law of total probability:Where P(Yᵢ = 1| Xᵢ, i ∈ Clusterⱼ) is given by j-th classification model fitted and P(i ∈ Clusterⱼ) comes from the cluster assignment classifier.3. Generalization to non-integer weightsGeneralization to non-integer weights relaxes the integer constraint on the z variables. This corresponds to the case of an algorithm allowing for (probabilistic) assignment to multiple clusters, e.g. Soft K-Means — in this case assignments become weights between 0 and 1.The fitting and inference processes are very similar to previously, with the sole differences being during the fitting phase: calibrating the regression / classification models on each cluster is replaced with calibrated the weighted regressions (e.g. Weighted Least Squares) or weighted classifications (e.g. Weighted Logistic Regression — see [4] for an example), with weight matrices Wⱼ = Diag(zᵢⱼ) with i corresponding to all the indices such that zᵢⱼ > 0. Note that unlike methods such as Weighted Least Squares, weights here are given when fitting the regression.This generalization has 2 direct implications on the problem at hand:Being a less constrained optimization problem, it will naturally yield a better solution, i.e. a lower loss in-sample than the integer-constrained versionIt will be more prone to overfitting, therefore bringing the need for increased regularization[1] already included a regularization term for the regression coefficients, which corresponds to having regularized fⱼ models: in the case of a Linear Regression, this would means for instance that fⱼ is a LASSO or a Ridge rather than a simple OLS.Yet, the proposal here is different, as we suggest additional regularization, this time penalizing the non-zero zᵢⱼ: the rationale is that we want to limit the number of models implicated in the fitting / inference of a given data point to reduce noise and degrees of freedom to prevent overfitting.In practice, we add a new set of binary variables (bᵢⱼ) equal to 1 if zᵢⱼ > 0 and 0 otherwise. We can write it as linear constraints using the big M method:All in, we have the two optimization models:Generalized Cluster While Regress:Generalized Cluster While Classify:These problems can be efficiently solved with First Order methods or Cutting Planes — see [3] for details.4. Evaluation:We evaluate these methods on 3 different benchmark datasets to illustrate 3 key aspects of their behavior and performance:Propension to overfitBetter performance when data is imbalanced or asymmetric — i.e. bigger consequences in cases of false positive or false negativeBetter performance in low data settingsSome implementation details:Given that all the methods presented are agnostic to the type of classification model used, we will assume the same classifier across the board to ensure fair comparison. For simplicity, we choose Logistic Regression with L2 regularization (which is the base setting in Scikit-Learn).For Cluster Then Classify (CTC), we use the K-Means clustering algorithm. We choose the number of clusters that maximizes the silhouette score of the clustering.For Cluster While Classify (CWC), we choose the number of clusters by cross-validation, i.e. the number of clusters that maximizes the AUC of the ROC curve on a validation dataset. We then re-fit the chosen model on both train and validation datasets. If the optimal number of clusters is 2, we opt for the CWC with integer weights for parsimony.Inference for CTC and CWC is done with using process Model Inference presented earlier, i.e. a weighted sum of the probabilities predicted by each sub-model.4.1 UCI Diabetes 130 datasetThe Diabetes 130-US Hospitals dataset (1999–2008) ([5]) contains information about diabetes patients admitted to 130 hospitals across the United States over a 9-year period. The goal of the classification task is to predict whether a given diabetes patient will be readmitted. We will simplify the classes into 2 classes — readmitted or not — instead of 3 (readmitted after less than 30 days, readmitted after more than 30 days, not readmitted). We will also consider a subset of 20,000 data points instead of the full 100,000 instances for faster training.4.2 UCI MAGIC Gamma Telescope datasetThe MAGIC Gamma Telescope dataset ([6]) contains data from an observatory aimed at classifying high-energy cosmic ray events as either gamma rays (signal) or hadrons (background). A specificity of this dataset is the non-symmetric nature of errors: given the higher cost of false positives (misclassifying hadrons as gamma rays), accuracy is not suitable. Instead, performance is evaluated using the ROC curve and AUC, with a focus on maintaining a false positive rate (FPR) below 20% — as explained in [6].4.3 UCI Parkinsons datasetThe Parkinson’s dataset ([7]) contains data collected from voice recordings of 195 individuals, including both those with Parkinson’s disease and healthy controls. The dataset is used for classifying the presence or absence of Parkinson’s based on features extracted from speech signals. A key challenge of this dataset is the low number of datapoints, which makes generalization with traditional ML methods difficult. We can diagnose this generalization challenge and overfitting by comparing the performance numbers on train vs test sets.ConclusionThe study of baseline and joint clustering and classification approaches demonstrates that choice of method depends significantly on the characteristics of the data and the problem setting — in short, there is no one-size-fits-all model.Our findings highlight key distinctions between the approaches studied across various scenarios:In traditional settings, i.e. large datasets, numerous features and balanced outcomes, conventional machine learning models generally perform well. The added step of clustering offers minor benefits, but the potential for overfitting with methods like CWC may lead to worse performance on unseen data.In non-traditional settings with asymmetric error consequences, where false positives or false negatives carry unequal costs, methods like CWC provide some advantage. By tailoring predictions to cluster-specific dynamics, CWC seems to better aligns with the loss function’s priorities.In low-data environments, the benefits of joint clustering and prediction become particularly pronounced. While traditional models and CTC approaches often struggle with overfitting due to insufficient data, CWC outperforms by extracting more information from what is available. Its iterative optimization framework enables better generalization and robustness in these challenging scenarios.Appendix:CWR on the log odds for Logistic RegressionStarting with the log odds of Logistic Regression in the CWR form:This yields the probabilities:Reinjecting these expressions in the likelihood function of Logistic Regression:And the log-likelihood:This yields the same objective function as CWC when constraining the zᵢⱼ to be binary variables.References:[1] L. Baardman, I. Levin, G. Perakis, D. Singhvi, Leveraging Comparables for New Product Sales Forecasting (2018), Wiley[2] L. Baardman, R. Cristian, G. Perakis, D. Singhvi, O. Skali Lami, L. Thayaparan, The role of optimization in some recent advances in data-driven decision-making (2023), Springer Nature[3] D. Bertsimas, J. Dunn, Machine Learning Under a Modern Optimization Lens (2021), Dynamic Ideas[4] G. Zeng, A comprehensive study of coefficient signs in weighted logistic regression (2024), Helyion[5] J. Clore, K. Cios, J. DeShazo, B. Strack, Diabetes 130-US Hospitals for Years 1999–2008 [Dataset] (2014), UCI Machine Learning Repository (CC BY 4.0)[6] R. Bock, MAGIC Gamma Telescope [Dataset] (2004), UCI Machine Learning Repository (CC BY 4.0)[7] M. Little, Parkinsons [Dataset] (2007). UCI Machine Learning Repository (CC BY 4.0)[8] D. Bertsimas, N. Kallus, From Predictive to Prescriptive Analytics (2019), INFORMSCluster While Predict: Iterative Methods for Regression and Classification was originally published in Towards Data Science on Medium, where people are continuing the conversation by highlighting and responding to this story. clustering, classification, machine-learning, optimization, prescriptive-analytics Towards Data Science – MediumRead More

 Add to favorites
Add to favorites


0 Comments